Question

8．⊙O的半径为10cm，AB，CD是⊙O的两条弦，AB∥CD，AB=12cm，CD=16cm，求AB和CD之间的距离．

Answer 1

分析 分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可．

解答 解：①当弦AB和CD在圆心同侧时，如图1所示，
∵AB=12cm，CD=16cm，
∴AF=6cm，CE=8cm，
∵OA=OC=10cm，
∴EO=6cm，OF=8cm，
∴EF=OF-OE=2cm；
②当弦AB和CD在圆心异侧时，如图2所示，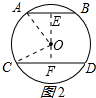
∵AB=12cm，CD=16cm，
∴AE=6cm，CF=8cm，
∵OA=OC=10cm，
∴EO=8cm，OF=6cm，
∴EF=OF+OE=14cm；
综上所述：AB和CD之间的距离为2cm或14cm．

点评 本题考查了勾股定理和垂径定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算，注意分两种情况讨论．