题目内容
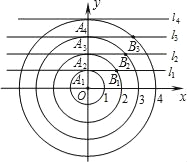
【题目】如图，在平面直角坐标系xOy中，点A1，A2，A3，…都在y轴上，对应的纵坐标分别为1，2，3，…．直线l1，l2，l3，…分别经过点A1，A2，A3，…，且都平行于x轴．以点O为圆心，半径为2的圆与直线l1在第一象限交于点B1，以点O为圆心，半径为3的圆与直线l2在第一象限交于点B2，…，依此规律得到一系列点Bn（n为正整数），则点B1的坐标为_____，点Bn的坐标为_____．
【答案】（
，1） （
，n）
【解析】
作辅助线,利用勾股定理即可求出坐标.
连OB1，OB2，OB3，如图，
在Rt△OA1B1中，OA1＝1，OB1＝2，
∴A1B1＝
＝
＝，
∴B1的坐标为（，1），
故答案为：（，1）；
在Rt△OA2B2中，OA2＝2，OB2＝3，
∴A2B2＝
∴B2的坐标为（，2）
在Rt△OA3B3中，OA3＝3，OB3＝4，
∴A3B3＝
，
∴B3的坐标为（
，3）；
…按照此规律可得点Bn的坐标是（
，n），即（，n）
故答案为：（，n）．
练习册系列答案
相关题目
