Question

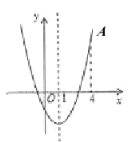
【题目】二次函数（）的大致图象如图所示，顶点坐标为，点是该抛物线上一点，若点是抛物线上任意一点，有下列结论：

①；

②若，则；

③若，则；

④若方程有两个实数根和，且，则．

其中正确结论的个数是（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

由抛物线对称轴为：直线x=1，得x=-2与x=4所对应的函数值相等，即可判断①；由由抛物线的对称性即可判断②；由抛物线的顶点坐标为，结合函数的图象，直接可判断③；由方程有两个实数根和，且，得抛物线与直线的交点的横坐标为和，进而即可判断④．

∵抛物线顶点坐标为，

∴抛物线对称轴为：直线x=1，

∴x=-2与x=4所对应的函数值相等，即：，

∴①正确；

由抛物线的对称性可知：若，则或，

∴②错误；

∵抛物线的顶点坐标为，

∴时，，

∴③错误；

∵方程有两个实数根和，且，

∴抛物线与直线的交点的横坐标为和，

∵抛物线开口向上，与x轴的交点横坐标分别为：-1，3，

∴，

∴④正确．

故选B．