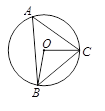
题目内容
如图①,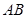 为⊙
为⊙ 的直径,
的直径,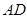 与⊙
与⊙ 相切于点
相切于点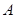 ,
,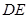 与⊙
与⊙ 相切于点
相切于点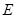 ,点
,点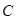 为
为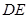 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.

(1)求证: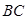 为⊙
为⊙ 的切线;
的切线;
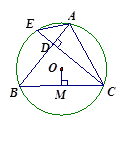
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G.若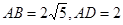 ,求线段BC和EG的长.
,求线段BC和EG的长.
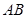 为⊙
为⊙ 的直径,
的直径,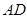 与⊙
与⊙ 相切于点
相切于点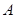 ,
,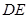 与⊙
与⊙ 相切于点
相切于点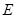 ,点
,点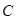 为
为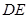 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.
(1)求证:
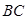 为⊙
为⊙ 的切线;
的切线;(2)如图②,连接AE,AE的延长线与BC的延长线交于点G.若
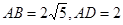 ,求线段BC和EG的长.
,求线段BC和EG的长.(1)连接OE、OC,先根据“SSS”证得△OBC≌△OEC,即得∠OBC=∠OEC,再结合DE为⊙O的切线即可证得结论;(2)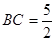 ,
,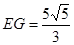
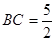 ,
,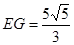
试题分析:(1)连接OE、OC,先根据“SSS”证得△OBC≌△OEC,即得∠OBC=∠OEC,再结合DE为⊙O的切线即可证得结论;
(2)过点D作DF⊥BC于点F,先根据切线的性质可得DA=DE,CE=CB,设BC为
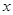 ,则CF=x-2,DC=x+2,在Rt△DFC中根据勾股定理即可列方程求得x的值,根据平行线的性质可得∠DAE=∠EGC,再根据等边对等角可得∠DAE=∠AED,即可得到∠ECG=∠CEG,从而可以求得BG的长,再根据勾股定理即可AG的长,然后证得△ADE∽△GCE,根据相似三角形的性质即可求得结果.
,则CF=x-2,DC=x+2,在Rt△DFC中根据勾股定理即可列方程求得x的值,根据平行线的性质可得∠DAE=∠EGC,再根据等边对等角可得∠DAE=∠AED,即可得到∠ECG=∠CEG,从而可以求得BG的长,再根据勾股定理即可AG的长,然后证得△ADE∽△GCE,根据相似三角形的性质即可求得结果.(1)连接OE、OC
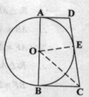
∵CB=CE,OB=OE,OC=OC
∴△OBC≌△OEC
∴∠OBC=∠OEC
又∵DE与⊙O相切于点
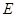
∴∠OEC=90°
∴∠OBC=90°
∴BC为⊙
 的切线;
的切线;(2)过点D作DF⊥BC于点F,
∵AD、DC、BG分别切⊙O于点A、E、B
∴DA=DE,CE="CB"
设BC为
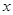 ,则CF=x-2,DC=x+2
,则CF=x-2,DC=x+2在Rt△DFC中,
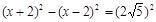
解得
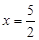
∵AD∥BG
∴∠DAE=∠EGC
∵DA=DE
∴∠DAE=∠AED
∵∠AED=∠CEG
∴∠ECG=∠CEG
∴CG=CE=CB=
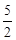
∴BG=5
∴
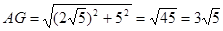
∵∠DAE=∠EGC,∠AED=∠CEG
∴△ADE∽△GCE
∴
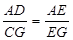 ,即
,即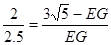 ,解得
,解得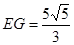 .
.点评:在证明切线的问题时,一般先连接切点与圆心,再证明垂直即可.

练习册系列答案
相关题目
 、
、 、
、 是⊙O上的三点,
是⊙O上的三点, .
.
 平分
平分 ;
; 作
作 于点
于点 ,交
,交 . 若
. 若 ,
, ,求
,求 的长.
的长.
 cm2,则扇形的弧长为________
cm2,则扇形的弧长为________  的直径
的直径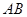 为10cm,弦
为10cm,弦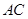 为6cm,
为6cm,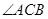 的平分线交
的平分线交 ,交
,交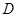 .求弦
.求弦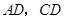 的长及
的长及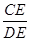 的值.
的值.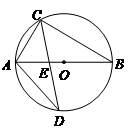
 .
.