题目内容
 如图,AB=5cm是⊙O的直径,弦BC=3cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发以1cm/s沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t=
如图,AB=5cm是⊙O的直径,弦BC=3cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发以1cm/s沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t=| 20 |
| 13 |
| 25 |
| 14 |
| 20 |
| 13 |
| 25 |
| 14 |
分析:应分两种情况进行讨论:①当PQ⊥AC时,△APQ为直角三角形,根据△APQ∽△ABC,可将时间t求出;当PQ⊥AB时,△APQ为直角三角形,根据△APQ∽△ACB,可将时间t求出.
解答: 解:如图,∵AB是直径,
解:如图,∵AB是直径,
∴∠C=90°.
又∵AB=5cm,BC=3cm,
∴根据勾股定理得到AC=
=4cm.
则AP=(5-2t)cm,AQ=t.
∵当点P到达点A时,点Q也随之停止运动,
∴0<t≤2.5.
①如图1,当PQ⊥AC时,PQ∥BC,则
△APQ∽△ABC.
故
=
,即
=
,解得t=
.
②如图2,当PQ⊥AB时,△APQ∽△ACB,则
=
,即
=
,
解得t=
.
综上所述,当t=
s或t=
时,△APQ为直角三角形.
故答案是:
或
.
 解:如图,∵AB是直径,
解:如图,∵AB是直径,∴∠C=90°.
又∵AB=5cm,BC=3cm,
∴根据勾股定理得到AC=
| AB2-BC2 |
则AP=(5-2t)cm,AQ=t.
∵当点P到达点A时,点Q也随之停止运动,
∴0<t≤2.5.
①如图1,当PQ⊥AC时,PQ∥BC,则

△APQ∽△ABC.
故
| AQ |
| AC |
| AP |
| AB |
| t |
| 4 |
| 5-2t |
| 5 |
| 20 |
| 13 |
②如图2,当PQ⊥AB时,△APQ∽△ACB,则
| AP |
| AC |
| AQ |
| AB |
| 5-2t |
| 4 |
| t |
| 5 |
解得t=
| 25 |
| 14 |
综上所述,当t=
| 20 |
| 13 |
| 25 |
| 14 |
故答案是:
| 20 |
| 13 |
| 25 |
| 14 |
点评:本题考查圆周角定理、相似三角形的性质、直角三角形的性质等知识的综合应用能力.在求时间t时应分情况进行讨论,防止漏解.

练习册系列答案
相关题目
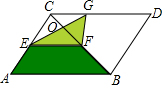 如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积.
如图,点F是菱形ABDC对角线BC上一动点,EF∥AB,GF∥AC,菱形两条对角线BC和AD的长分别为2cm、5cm,当点F在BC上移动时,阴影面积会改变吗?如果不变,请求出阴影部分的面积. 如图,AB是⊙O的直径,弦CD⊥AB于点P,CD=8cm,OP=3cm,那么⊙O的半径等于( )
如图,AB是⊙O的直径,弦CD⊥AB于点P,CD=8cm,OP=3cm,那么⊙O的半径等于( ) 如图,AB=AC,AB的垂直平分线MN交AC于点D,AB=8cm,BC=5cm,则△DBC的周长是
如图,AB=AC,AB的垂直平分线MN交AC于点D,AB=8cm,BC=5cm,则△DBC的周长是 如图,AB=5cm是⊙O的直径,弦BC=3cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发以1cm/s沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t=________.
如图,AB=5cm是⊙O的直径,弦BC=3cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q从A点出发以1cm/s沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t=________.