题目内容
△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,以R长为半径画圆,若⊙C与AB相交,求R的范围.
【答案】分析:根据直线和圆相交的位置关系与数量关系之间的联系,可知此题解决的关键是求得点C到AB的距离.同时圆与线段AB相交时,半径要小于或等于AC的长,由此可解.
解答: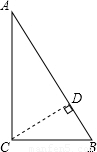 解:作CD⊥AB于D.
解:作CD⊥AB于D.
∵∠C=90°,AC=4,BC=3,
由勾股定理得:AB=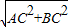 =
=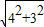 =5;
=5;
由面积公式得: ×AC×BC=
×AC×BC= ×AB×CD,
×AB×CD,
∴CD=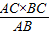 =
=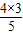 =2.4;
=2.4;
∴当2.4<R≤4时,⊙C与AB相交.
点评:本题考查了直线和圆的位置关系.设圆心到直线的距离为d,半径为r,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交;所以解决此类问题的关键是确定圆心到直线的距离.本题注意是圆与线段AB相交.
解答:
 解:作CD⊥AB于D.
解:作CD⊥AB于D.∵∠C=90°,AC=4,BC=3,
由勾股定理得:AB=
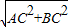 =
=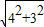 =5;
=5;由面积公式得:
 ×AC×BC=
×AC×BC= ×AB×CD,
×AB×CD,∴CD=
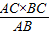 =
=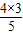 =2.4;
=2.4;∴当2.4<R≤4时,⊙C与AB相交.
点评:本题考查了直线和圆的位置关系.设圆心到直线的距离为d,半径为r,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交;所以解决此类问题的关键是确定圆心到直线的距离.本题注意是圆与线段AB相交.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )
如图,在△ABC中,AC=2,AB=3,D是AC上一点,E是AB上一点,且∠ADE=∠B,设AD=x,AE=y,则y与x之间的函数关系式是( )A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
 如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,
如图,在△ABC中,AB=8,AC=6,BC=7,点D在AC上,AD=2,