题目内容
△ABC中，AC=AB，BD为△ABC的高，如果∠ABD=25°，则∠C=
- A.65°
- B.52.5°
- C.50°
- D.57.5°
D
分析：根据BD为△ABC的高，∠ABD=25°，利用三角形内角和定理求出∠A，再根据等腰三角形的性质和三角形内角和定理即可求得∠C．
解答：∵BD为△ABC的高，∠ABD=25°，
∴∠A=90°-∠ABD=25°=65°，
∵AB=AC，
∴∠C=∠ABC，
∴∠C=
（180-∠A）=（180-65）=57.5°．
故选D．
点评：此题主要考查等腰三角形的性质和三角形内角和定理等知识点，难度不大，属于基础题．
分析：根据BD为△ABC的高，∠ABD=25°，利用三角形内角和定理求出∠A，再根据等腰三角形的性质和三角形内角和定理即可求得∠C．
解答：∵BD为△ABC的高，∠ABD=25°，
∴∠A=90°-∠ABD=25°=65°，
∵AB=AC，
∴∠C=∠ABC，
∴∠C=
（180-∠A）=（180-65）=57.5°．故选D．
点评：此题主要考查等腰三角形的性质和三角形内角和定理等知识点，难度不大，属于基础题．
练习册系列答案
相关题目
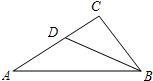如图，在△ABC中，AC＞BC，D是AC边上一点，连接BD．
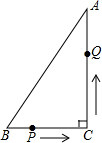如图，在Rt△ABC中，AC=24cm，BC=7cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5cm/s．若点P、Q分别从B、C同时运动，且运动时间记为t秒，请解答下面的问题，并写出探索的主要过程．