题目内容

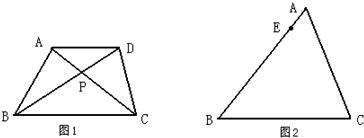
如图4，在梯形ABCD中，AD∥BC，AC⊥AB，AD=CD，cosB=，BC=26．

求：

1.cos∠DAC的值；

2.线段AD的长

 

 

1.

2.13

解析:（1）由cosB=和BC=26，可求得，AB=10

可证得：∠ACB=∠ACD=∠DAC，由勾股定理可求得AC=24，

∴cos∠DAC=cos∠ACB=.

（2）取AC中点E，连接DE，AE=12，cos∠DAC=.

由等腰△ADC三线合一得DE⊥AC，∴Rt△AED中AD=AE/cos∠DAC=13.

 

练习册系列答案
相关题目
24、如图1，在梯形ABCD中AD∥BC，对角线AC，BD交于点P，则s△PAB=S△PDC，请你用梯形对角线的这一特殊性质，解决下面问题．
在图2中，点E是△ABC中AB边上的任意一点，且AE≠BE，过点E画一条直线，把△ABC分成面积相等的两部分，保留作图痕迹，并简要说明你的方法．
如图1，在Rt△ABC中，∠A=90°，AB=AC，BC=4
2
，另有一等腰梯形DEFG（GF∥DE）的底边DE与BC重合，两腰分别落在AB，AC上，且G，F分别是AB，AC的中点．
精英家教网
（1）求等腰梯形DEFG的面积；
（2）操作：固定△ABC，将等腰梯形DEFG以每秒1个单位的速度沿BC方向向右运动，直到点D与点C重合时停止．设运动时间为x秒，运动后的等腰梯形为DEF′G′（如图2）．
探究1：在运动过程中，四边形BDG′G能否是菱形？若能，请求出此时x的值；若不能，请说明理由；
探究2：设在运动过程中△ABC与等腰梯形DEFG重叠部分的面积为y，求y与x的函数关系式．
24、如图，已知：AD是△ABC中BC边的中线，则S△ABD=S△ACD，依据是
等底等高的三角形面积相等

规定；若一条直线l把一个图形分成面积相等的两个图形，则称这样的直线l叫做这个图形的等积直线．根据此定义，在图1中易知直线为△ABC的等积直线．
（1）如图2，在矩形ABCD中，直线l经过AD，BC边的中点M、N，请你判断直线l是否为该矩形的等积直线
是
（填“是”或“否”）．在图2中再画出一条该矩形的等积直线．（不必写作法）
（2）如图3，在梯形ABCD中，直线l经过上下底AD、BC边的中点M、N，请你判断直线l是否为该梯形的等积直线
是
（填“是”或“否”）．
（3）在图3中，过M、N的中点O任作一条直线PQ分别交AD，BC于点P、Q，如图4所示，猜想PQ是否为该梯形的等积直线？请说明理由．
（2012•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN
（1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=
1
2
∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．
（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=
1
2
∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．
（2013•乐山）阅读下列材料：
如图1，在梯形ABCD中，AD∥BC，点M，N分别在边AB，DC上，且MN∥AD，记AD=a，BC=b．若
AM
MB
=
m
n
，则有结论：MN=
bm+an
m+n
．
请根据以上结论，解答下列问题：
如图2，图3，BE，CF是△ABC的两条角平分线，过EF上一点P分别作△ABC三边的垂线段PP1，PP2，PP3，交BC于点P1，交AB于点P2，交AC于点P3．
（1）若点P为线段EF的中点．求证：PP1=PP2+PP3；
（2）若点P为线段EF上的任意位置时，试探究PP1，PP2，PP3的数量关系，并给出证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网