题目内容
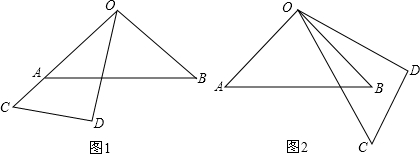
附加题:已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠COD=30°)如图1摆放,点O、A、C在一条直线上.将直角三角板OCD绕点O逆时针方向转动,变化摆放如图位置
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是
(2)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
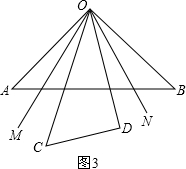
(3)当三角板OCD从图1的位置开始,绕点O逆时针方向旋转一周,保持射线OM平分∠AOC、射线ON平分∠BOD(∠AOC≤180°,∠BOD≤180°),在旋转过程中,(2)中的结论是否保持不变?如果保持不变,请说明理由;如果变化,请说明变化的情况和结果(即旋转角度a在什么范围内时∠MON的度数是多少).
分析:利用三角板角的特征和角平分线的定义解答:
(1)由图可得角之间的关系:∠BOD=90°-∠COD,∠AOC=90°-
∠COD,据此解答;
(2)由图可得角之间的关系:∠MON=
(∠AOB-∠COD)+∠COD;
(3)可分以下情况考虑:①当0°<α<180°时;②α=180°时,两种情况:点M在OB上和点M在BO上;③180°<α<240°时;④α=240°,⑤240°<α<360°时五种情况讨论.
(1)由图可得角之间的关系:∠BOD=90°-∠COD,∠AOC=90°-
| 1 |
| 2 |
(2)由图可得角之间的关系:∠MON=
| 1 |
| 2 |
(3)可分以下情况考虑:①当0°<α<180°时;②α=180°时,两种情况:点M在OB上和点M在BO上;③180°<α<240°时;④α=240°,⑤240°<α<360°时五种情况讨论.
解答:解:(1)∠BOD=90°-∠COD=90°-30°=60°,
∠AOC=90°-
∠COD=90°-
×30°=75°.
(2)不变,60°.
根据图中所示∠MON=
(∠AOB-∠COD)+∠COD=
(90°-30°)+30°=60度.
(3)①当0°<α<180°时,
∠MON=
(90°+∠BOC)+
(30°+∠BOC)-∠BOC=60°
②α=180°时,即∠AOC为平角,
(1)点M在OB上,
∴∠MOD=∠BOC+∠COD=90°+30°=120°,
又∵ON平分∠BOD,
∴∠MON=120×
=60度.
(2)点M在BO上,
∠MON=180°-60°=120度.
故∠MON=60°或120°
③180°<α<240°时,
2(30°+∠MOD)+90°+∠CON+(∠CON+30°)=360°,
解得:∠MOD+∠CON=90°,则
∠MON=90°+30°=120°
③当α=240°时,∠BOD=180°,那么此时N可以平分在∠BOD的左边,使得∠MON=60°,N平分在∠BOD的右边,那么∠MON=120°
⑤240°<α<360°时,
∠MON=
(30°-∠AOD)+
(90°-∠AOD)+∠AOD=60度.
∠AOC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
(2)不变,60°.
根据图中所示∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
(3)①当0°<α<180°时,
∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
②α=180°时,即∠AOC为平角,
(1)点M在OB上,
∴∠MOD=∠BOC+∠COD=90°+30°=120°,
又∵ON平分∠BOD,
∴∠MON=120×
| 1 |
| 2 |
(2)点M在BO上,
∠MON=180°-60°=120度.
故∠MON=60°或120°
③180°<α<240°时,
2(30°+∠MOD)+90°+∠CON+(∠CON+30°)=360°,
解得:∠MOD+∠CON=90°,则
∠MON=90°+30°=120°
③当α=240°时,∠BOD=180°,那么此时N可以平分在∠BOD的左边,使得∠MON=60°,N平分在∠BOD的右边,那么∠MON=120°
⑤240°<α<360°时,
∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题很复杂,难点是找出变化过程中的不变量,需要结合图形来计算,对同学们的作图、分析、计算能力有较高要求.在计算分析的过程中注意动手操作,在旋转的过程中得到不变的量.

练习册系列答案
相关题目
已知∠α是一副三角板中的某个锐角,则( )
| A、sinα>cosα | B、sinα<cosα | C、sinα=cosα | D、以上三种都有可能 |


