题目内容
 已知长方形ABCD,将BCD沿对角线BD折叠,记点C的对应点为C′,若∠ADC′=40°,则∠BDC的度数为
已知长方形ABCD,将BCD沿对角线BD折叠,记点C的对应点为C′,若∠ADC′=40°,则∠BDC的度数为65°
65°
.分析:由折叠的性质可知∠BDC=∠BDC′,故∠ADB=∠BDC′-∠ADC′=∠BDC-40°,根据∠ADB+∠BDC=90°,列方程求∠BDC.
解答:解:由折叠的性质,得∠BDC=∠BDC′,
则∠ADB=∠BDC′-∠ADC′=∠BDC-40°,
∵∠ADB+∠BDC=90°,
∴∠BDC-40°+∠BDC=90°,
解得∠BDC=65°.
故答案为65°.
则∠ADB=∠BDC′-∠ADC′=∠BDC-40°,
∵∠ADB+∠BDC=90°,
∴∠BDC-40°+∠BDC=90°,
解得∠BDC=65°.
故答案为65°.
点评:本题利用了折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
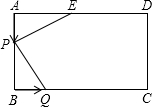 等?
等?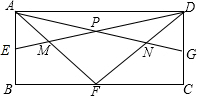 如图,在长方形ABCD中,E、F、G分别是边AB、BC、CD的中点.已知长方形ABCD的面积是40cm2.则四边形MFNP的面积是
如图,在长方形ABCD中,E、F、G分别是边AB、BC、CD的中点.已知长方形ABCD的面积是40cm2.则四边形MFNP的面积是 如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2
如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2 如图所示,已知长方形ABCD,点A′是长方形ABCD平移后点A的对应点,作出平移后的长方形A′B′C′D′.
如图所示,已知长方形ABCD,点A′是长方形ABCD平移后点A的对应点,作出平移后的长方形A′B′C′D′.