题目内容
 如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2
如图,已知长方形ABCD四个顶点的坐标分别是A(2,-2| 2 |
| 2 |
| 2 |
| 2 |
(1)求四边形ABCD的面积是多少?
(2)将四边形ABCD向上平移2
| 2 |
分析:(1)先根据A、B、C、D四个顶点的坐标分别求出AB、AD,再根据长方形的面积公式即可求解;
(2)根据平移性质把各个点的纵坐标加上2
即可得出答案.
(2)根据平移性质把各个点的纵坐标加上2
| 2 |
解答:解:(1)∵A(2,-2
),B(5,-2
),C(5,-
),D(2,-
).
∴AB=5-2=3,AD=-
+2
=
,
∴四边形ABCD的面积为:AB×AD=3
;
(2)∵A(2,-2
),B(5,-2
),C(5,-
),D(2,-
),
∴将这个四边形向上平移2
个单位长度,四个顶点的坐标变为A′(2,0),B′(5,0),C′(5,
),D′(2,
).
| 2 |
| 2 |
| 2 |
| 2 |
∴AB=5-2=3,AD=-
| 2 |
| 2 |
| 2 |
∴四边形ABCD的面积为:AB×AD=3
| 2 |
(2)∵A(2,-2
| 2 |
| 2 |
| 2 |
| 2 |
∴将这个四边形向上平移2
| 2 |
| 2 |
| 2 |
点评:本题考查了矩形的性质和判定,平移的性质,关键是能熟练地运用性质进行计算.

练习册系列答案
相关题目
 48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M.
48、如图,已知长方形的台球桌台ABCD,有黑、白两球分别位于M、N两点的位置上,试问:怎样撞击白球N,才能让白球先撞台边AB,反弹后再击中黑球M. 8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )
8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( ) 如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=
如图,已知长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则EF=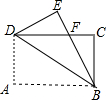 如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为
如图,已知长方形ABCD沿着直线BD折叠,使点A落在点E处,EB交DC于F,BC=3,AB=4,则点F到直线DB的距离为 如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互
如图,已知长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互