��Ŀ����
��ͼ1��������y= 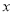 2+b
2+b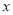 +c��x�ύ��A��-1,0����B��3��0�����㣬��y�ύ�ڵ�C.
+c��x�ύ��A��-1,0����B��3��0�����㣬��y�ύ�ڵ�C.
��1����������ߵĽ���ʽ��
��2����M�������ߵĶԳ�����ֱ��BC�Ľ��㣬N�������ߵĶ��㣬��MN�ij���
��3�����P�ǣ�1���е������ߵ�һ�����㣬�Ƿ��������S��PAB=8�ĵ�P������������P�����ꣻ�������ڣ���˵������.
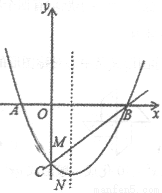
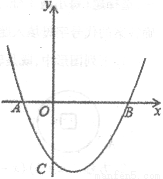
ͼ1 ����ͼ
��1��y=x2��2x��3����2��1����3����P�������ֱ�Ϊ��1+2��4������1��2��4������1����4��ʱ��S��PAB=8�� �������������������1���ѵ�A��B������ֱ���뺯������ʽ���г�����ϵ��b��c�ķ����飬ͨ���ⷽ����������ǵ�ֵ���ɣ� ��2����������ߵĽ���ʽ�õ���C��N�����꣬����B��C������������ֱ��BC�Ľ���ʽ����һ�κ���ͼ���ϵ�����������͵��������ͼ�ε����ʽ��н�...
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ


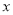 ��ԳƵġ�A1B1C1��
��ԳƵġ�A1B1C1��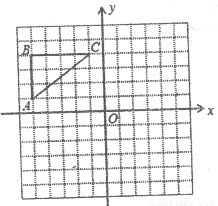
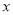 �ķ���
�ķ���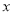 2-2
2-2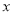 -1=0��һ��������2m2-4m+2017= .
-1=0��һ��������2m2-4m+2017= .