��Ŀ����
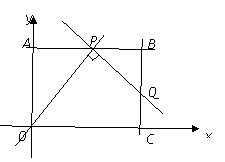
��ͼ����ƽ��ֱ������ϵ�У��ı���![]() Ϊ���Σ�
����![]() ��
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ���㣬��ֱ��
��һ���㣬��ֱ��![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת
��ʱ�뷽����ת![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ��
��
 ��1������
��1������![]() ���߶�
���߶�![]() ���˶�������
���˶�������![]() �غϣ�ʱ��
�غϣ�ʱ��
��֤��OA·BQ=AP·BP��
 ��2���ڣ�1�������������£����
��2���ڣ�1�������������£����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
�߶�![]() �ij���Ϊ
�ij���Ϊ![]() �����
�����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
���ж�![]() �Ƿ������Сֵ�������ڣ��������Сֵ��
�Ƿ������Сֵ�������ڣ��������Сֵ��
�������ڣ���˵�����ɡ�
��3��ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ�
Ϊ���������Σ������ڣ�
�������![]() �����ꣻ�������ڣ���˵�����ɡ�
�����ꣻ�������ڣ���˵�����ɡ�
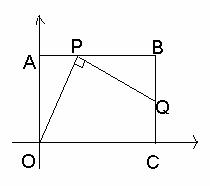
 ��1��֤�������ı���OABCΪ����
��1��֤�������ı���OABCΪ����
���OAP=��QBP=90��,
�ߡ�OPQ=90��, ���APO+��BPQ=90![]() =��APO+��AOP
=��APO+��AOP
���BPQ=��AOP, ���AOP�ס�BPQ
��![]()
��OA·BQ=AP·BP ----------------------3��
(2) �ɣ�1��֪OA·BQ=AP·BP ��3��BQ=m(4-m) ��BQ=![]()
��CQ=3-![]() =
=![]()
 ��L=
��L=![]() (0��m��4)
(0��m��4)
= ![]()
�൱m=2 ʱ�� L����С��=![]() -----------------6��
-----------------6��
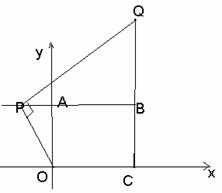
(3)�ߡ�OPQ=90��,��Ҫʹ��POQΪ���������Σ���PO=PQ .
����P���߶�AB��ʱ����ͼ (1)
�� AOP�ա�BPQ ��PB=AO=3
�� ��AP=4-3=1
��![]() (1,3)
(1,3)
(ͼ1)
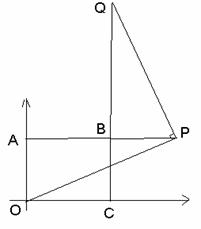
����P���߶�AB���ӳ�����ʱ����ͼ��2�� ![]()
��ʱ��QBP�ա�PAO
��PB=AO=3 ��AP=4+3=7
��![]() (7,3)
(7,3)
��ͼ2��
 ����P���߶�AB�ķ����ӳ�����ʱ����ͼ ��3��
����P���߶�AB�ķ����ӳ�����ʱ����ͼ ��3��
��ʱ��PB��AB��AO,
���PQB���������OPAȫ��,
��PQ��������PO���,
��ʱ��P������.
����������֪����![]() (1,3),
(1,3), ![]() (7,3). ---------------9��
(7,3). ---------------9��

 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��