Question

16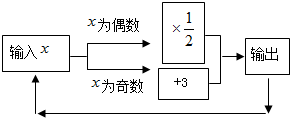．如图所示的运算程序中，
（1）若开始输入的x值为48，则第1次输出的结果为24，第2次输出的结果为12，…第2012次输出的结果为3．
（2）若经过一次输出的结果为-2，则输入的数x是多少？
（3）若输入一个数x经过两次输出的结果的和为12，请问x是多少？

Answer 1

分析 （1）根据输入的奇数和偶数代入计算，发现如果输出的次数大于3次，所得结果依次是3和6循环，且输出是奇数次时，结果是6，输出是偶数次时，结果是3；所以当输入的x=2012时，第2012次输出的结果为3；
（2）分奇数和偶数两种情况列等式进行计算．
（3）分奇数和偶数两种情况进行计算，要注意第二次输入时也要分奇数和偶数两种情况．

解答 解：（1）当输入的x=48时，第一次输出的结果为：48×$\frac{1}{2}$=24，
当输入的x=24时，第二次输出的结果为：24×$\frac{1}{2}$=12，
当输入的x=12时，第三次输出的结果为：12×$\frac{1}{2}$=6，
当输入的x=6时，第四次输出的结果为：6×$\frac{1}{2}$=3，
当输入的x=3时，第五次输出的结果为：3+3=6，
当输入的x=6时，第六次输出的结果为：6×$\frac{1}{2}$=3，
…
当输入的x=2012时，第2012次输出的结果为：3，
故答案为：12，3；
（2）当x是偶数时，$\frac{1}{2}$x=-2，x=-4，
当x是奇数时，x+3=-2，x=-5，
所以输入的数x是-4或-5；
（3）当x是偶数时，$\frac{1}{2}$x+$\frac{1}{4}$x=12或$\frac{1}{2}$x+$\frac{1}{2}$x+3=12，
解得：x=16或x=9（舍）
当x是奇数时，x+3+x+3+3=12或x+3+$\frac{1}{2}$（x+3）=12，
解得：x=$\frac{3}{2}$（舍）或5
所以输入的数x是16或5．

点评 本题既是代数式求值问题，也是一道找规律问题，要求学生细心观察、分析、归纳并发现其中的规律，也是一个易错题，要注意多计算几次输出的数；对于第3问中的数要分奇数和偶数两种情况进行计算．