题目内容
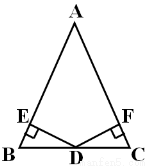
已知:如图,D是△ABC的BC边上的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF.求证: △ABC是等腰三角形.
证明见解析.
【解析】
试题分析:根据点D是△ABC的BC边上的中点,DE⊥AC于E,DF⊥AB于F,且DE=DF.利用HL求证△BFD≌△DEC,可得∠B=∠C,即可证明△ABC是等腰三角形.
试题解析:∵点D是△ABC的BC边上的中点,
∴BD=DC,
∵DE⊥AC于E,DF⊥AB于F,
∴△BFD和△DEC为直角三角形,
在Rt△BFD和Rt△CED中,
 ,
,
∴Rt△BFD≌Rt△CED(HL),
∴∠B=∠C,
∴△ABC是等腰三角形.
考点:1.等腰三角形的判定;2.全等三角形的判定与性质.

练习册系列答案
相关题目
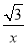 上的点B重合,若点B的纵坐标是1,则点A的坐标是
上的点B重合,若点B的纵坐标是1,则点A的坐标是 

 ,0 )为圆心,以2
,0 )为圆心,以2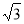 为半径的圆与x轴相交于点B、C,与y轴相交于点D、E
为半径的圆与x轴相交于点B、C,与y轴相交于点D、E
 经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上
经过C、D两点,求抛物线的表达式,并判断点B是否在该抛物线上

 +
+ 中自变量x的取值范围是( )
中自变量x的取值范围是( ) B.
B. C.
C. 且
且 D.
D. 且
且
 ,y1)、N(
,y1)、N( ,y2)、P(
,y2)、P( ,y3)三点都在函数
,y3)三点都在函数 (
( )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( )