题目内容
 (2013•钦州)如图,在平面直角坐标系中,O为坐标原点,抛物线y=
(2013•钦州)如图,在平面直角坐标系中,O为坐标原点,抛物线y=| 1 |
| 2 |
(1)求点A的坐标和∠AOB的度数;
(2)若将抛物线y=
| 1 |
| 2 |
(3)在(2)的情况下,判断点C′是否在抛物线y=
| 1 |
| 2 |
(4)若点P为x轴上的一个动点,试探究在抛物线m上是否存在点Q,使以点O、P、C、Q为顶点的四边形是平行四边形,且OC为该四边形的一条边?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
分析:(1)由y=
x2+2x得,y=
(x+2)2-2,故可得出抛物线的顶点A的坐标,令
x2+2x=0得出点B的坐标过点A作AD⊥x轴,垂足为D,由∠ADO=90°可知点D的坐标,故可得出OD=AD,由此即可得出结论;
(2)由题意可知抛物线m的二次项系数为
,由此可得抛物线m的解析式过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,根据勾股定理可求出OC的长,同理可得AC的长,OC=AC,由翻折不变性的性质可知,OC=AC=OC′=AC′,由此即可得出结论;
(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=-4代入抛物线y=
x2+2x进行检验即可得出结论;
(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a,
(a-2)2-4),由于OC为该四边形的一条边,故OP为对角线,由于点P在x轴上,根据中点坐标的定义即可得出a的值,故可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意可知抛物线m的二次项系数为
| 1 |
| 2 |
(3)过点C′作C′G⊥x轴,垂足为G,由于OC和OC′关于OA对称,∠AOB=∠AOH=45°,故可得出∠COH=∠C′OG,再根据CE∥OH可知∠OCE=∠C′OG,根据全等三角形的判定定理可知△CEO≌△C′GO,故可得出点C′的坐标把x=-4代入抛物线y=
| 1 |
| 2 |
(4)由于点P为x轴上的一个动点,点Q在抛物线m上,故设Q(a,
| 1 |
| 2 |
解答:解:(1)∵由y=
x2+2x得,y=
(x+2)2-2,
∴抛物线的顶点A的坐标为(-2,-2),
令
x2+2x=0,解得x1=0,x2=-4,
∴点B的坐标为(-4,0),
过点A作AD⊥x轴,垂足为D,
∴∠ADO=90°,
∴点A的坐标为(-2,-2),点D的坐标为(-2,0),
∴OD=AD=2,
∴∠AOB=45°;
(2)四边形ACOC′为菱形.
由题意可知抛物线m的二次项系数为
,且过顶点C的坐标是(2,-4),
∴抛物线的解析式为:y=
(x-2)2-4,即y=
x2-2x-2,
过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,
∴OE=2,CE=4,AF=4,CF=CE-EF=2,
∴OC=
=
=2
,
同理,AC=2
,OC=AC,
由翻折不变性的性质可知,OC=AC=OC′=AC′,
故四边形ACOC′为菱形.
(3)如图1,点C′不在抛物线y=
x2+2x上.
理由如下:
过点C′作C′G⊥x轴,垂足为G,
∵OC和OC′关于OA对称,∠AOB=∠AOH=45°,
∴∠COH=∠C′OG,
∵CE∥OH,
∴∠OCE=∠C′OG,
又∵∠CEO=∠C′GO=90°,OC=OC′,
∴△CEO≌△C′GO,
∴OG=CE=4,C′G=OE=2,
∴点C′的坐标为(-4,2),
把x=-4代入抛物线y=
x2+2x得y=0,
∴点C′不在抛物线y=
x2+2x上;
(4)存在符合条件的点Q.
∵点P为x轴上的一个动点,点Q在抛物线m上,
∴设Q(a,
(a-2)2-4),
∵OC为该四边形的一条边,
∴OP为对角线,
∴
=0,解得a1=6,a2=-2,
∴Q(6,4)或(-2,4)(舍去),
∴点Q的坐标为(6,4).
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线的顶点A的坐标为(-2,-2),
令
| 1 |
| 2 |
∴点B的坐标为(-4,0),

过点A作AD⊥x轴,垂足为D,
∴∠ADO=90°,
∴点A的坐标为(-2,-2),点D的坐标为(-2,0),
∴OD=AD=2,
∴∠AOB=45°;
(2)四边形ACOC′为菱形.
由题意可知抛物线m的二次项系数为
| 1 |
| 2 |
∴抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
过点C作CE⊥x轴,垂足为E;过点A作AF⊥CE,垂足为F,与y轴交与点H,
∴OE=2,CE=4,AF=4,CF=CE-EF=2,
∴OC=
| OE2+EC2 |
| 22+42 |
| 5 |
同理,AC=2
| 5 |
由翻折不变性的性质可知,OC=AC=OC′=AC′,
故四边形ACOC′为菱形.
(3)如图1,点C′不在抛物线y=
| 1 |
| 2 |
理由如下:
过点C′作C′G⊥x轴,垂足为G,
∵OC和OC′关于OA对称,∠AOB=∠AOH=45°,
∴∠COH=∠C′OG,
∵CE∥OH,
∴∠OCE=∠C′OG,
又∵∠CEO=∠C′GO=90°,OC=OC′,
∴△CEO≌△C′GO,
∴OG=CE=4,C′G=OE=2,
∴点C′的坐标为(-4,2),
把x=-4代入抛物线y=
| 1 |
| 2 |
∴点C′不在抛物线y=
| 1 |
| 2 |

(4)存在符合条件的点Q.
∵点P为x轴上的一个动点,点Q在抛物线m上,
∴设Q(a,
| 1 |
| 2 |
∵OC为该四边形的一条边,
∴OP为对角线,
∴
| ||
| 2 |
∴Q(6,4)或(-2,4)(舍去),
∴点Q的坐标为(6,4).
点评:本题考查的是二次函数综合题,涉及到抛物线的性质、菱形的判定与性质、平行四边形的性质等知识,难度适中.

练习册系列答案
相关题目
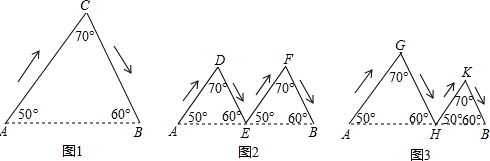
 (2013•钦州)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是
(2013•钦州)如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 (2013•钦州)如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.
(2013•钦州)如图,梯形ABCD中,AD∥BC,AB∥DE,∠DEC=∠C,求证:梯形ABCD是等腰梯形.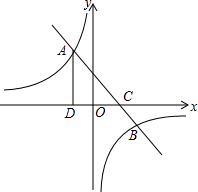 (2013•钦州)如图,一次函数y=ax+b的图象与反比例函数y=
(2013•钦州)如图,一次函数y=ax+b的图象与反比例函数y= (2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:
(2013•钦州)如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: