题目内容
在平行四边形ABCD中，AB=6，BC=10，∠A=150°，则?ABCD的面积为
- A.15
- B.18
- C.30
- D.60
C
分析：作平行四边形的高，然后求出即可求得平行四边形的面积．
解答：
解：如图：过A作AE⊥CD于E，
∵AB∥CD，∠BAD，∠D为同旁内角，
∴∠D=180-150=30°．
直角△AED中，AD=BC=10，
AE=AD•sinD=10×
=5．
∴S?ABCD=CD•AE=30．
故选C．
点评：解题关键是利用平行四边形的性质结合解直角三角形来解决有关的计算和证明．
分析：作平行四边形的高，然后求出即可求得平行四边形的面积．
解答：
解：如图：过A作AE⊥CD于E，∵AB∥CD，∠BAD，∠D为同旁内角，
∴∠D=180-150=30°．
直角△AED中，AD=BC=10，
AE=AD•sinD=10×
=5．∴S?ABCD=CD•AE=30．
故选C．
点评：解题关键是利用平行四边形的性质结合解直角三角形来解决有关的计算和证明．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
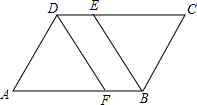如图，在平行四边形ABCD中，∠ABC的平分线交CD于点E，∠ADC的平分线交AB于点F．试判断AF与CE是否相等，并说明理由．
24、已知如图，在平行四边形ABCD中，BN=DM，BE=DF．求证：四边形MENF是平行四边形．
（2013•鞍山一模）在平行四边形ABCD中，∠DAB=60°，点E是AD的中点，点O是AB边上一点，且AO=AE，过点E作直线HF交DC于点H，交BA的延长线于F，以OE所在直线为对称轴，△FEO经轴对称变换后得到△F′EO，直线EF′交直线DC于点M．
如图，在平行四边形ABCD中，AE⊥AD交BD于点E，CF⊥BC交BD于点F．求证：BE=DF．
如图，在平行四边形ABCD中，∠B的平分线交AD于E，AE=10，ED=4，那么平行四边形ABCD的周长是