题目内容

如图1，图2，图3，在中，分别以为边，向外作正三角形，正四边形，正五边形，相交于点．（正多边形的各边相等，各个内角也相等）

（1）如图1，求证：．

（2）探究：如图1， ；如图2，　 ；如图3， 　 ．

如图4，已知：是以为边向外所作正边形的一组邻边；是以为边向外所作正边形的一组邻边．的延长相交于点．

猜想：如图4，　　　 （用含的式子表示）．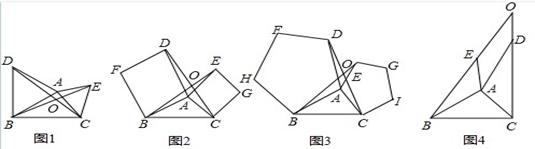

解：（1）∵△ABD、△ACE是等边三角形

∴AD=AB，AC=AE，∠BAD=∠CAE=60°

∴∠BAD+∠BAC=∠CAE+∠BAC，

即∠DAC=∠BAE

∴△ABE≌△ADC       

（2）120°；90°；72°；       

．               

练习册系列答案
相关题目
在平面直角坐标系xOy中，一动点P（x，y）从点M（1，0）出发，在由A（-1，1），B（-1，-1），C（1，-1），D（1，1）四点组成的正方形边线上（如图1所示），按一定方向匀速运动．图2是点P精英家教网运动的路程s与运动时间t（秒）之间的函数图象，图3是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分．
请结合以上信息回答下列问题：
（1）图②中，s与t之间的函数关系式是
 
（t≥0）；
（2）与图③中的折线段相对应的点P的运动路程是
 
→
 
→
 
→
 
；（填“A”、“B”、“C”、“D”、“M”、或“N”）
（3）当4≤s≤8时，直接写出y与s之间的函数关系式，并在图③中补全相应的函数图象．
如图（1），在Rt△ABC的边AB的同侧，分别以三边为直径作三个半圆，大半圆以外的两部分面积分别为S1、S3，三角形的面积为S2；
如图（2），两个反比例函数y=
2
x
和y=
1
x
在第一象限内的图象如图所示，点P在y=
2
x
的图象上，PC⊥x轴于点C，PD⊥y轴于点D，交y=
1
x
的图象于分别于点A，B，当点P在y=
2
x
的图象上运动时，△BOD，四边形OAPB，△AOC的面积分别为S1、S2、S3；
如图（3），点E为?ABCD边AD上任意一点，三个三角形的面积分别为S1、S2、S3；
如图（4），梯形ABCD中，AB∥CD，∠DAB+∠ABC=90°，AB=2CD，以AD、DC、CB为边作三个正方形的面积分别为S1、S2、S3．
在这四个图形中满足S1+S3=S2有
 
（填序号）．
精英家教网
如图，一架大型运输飞机从起飞开始到飞行10小时的时候，某空军加油飞机接到命令立即给运输飞机进行空中加油，设运输飞机的油箱余油量为Q1（吨），加油飞机从开始加油到加油结束的加油油箱耗油量为Q2（吨），运输飞机从起飞开始的飞行时间为t（小时），Q1（吨）、Q2（吨）与t（小时）之间的函数关系图象如图所示，若加油飞机与运输飞机每小时的耗油量相同，且运输飞机从起飞开始到降落一直保持匀速飞行，请结合图象，解答下列问题．
精英家教网（1）求运输飞机起飞时油箱的油量；
（2）求运输飞机从起飞开始油箱余油量Q1（吨）与飞行时间t（小时）之间的函数关系式；
（3）运输飞机加油后，以原来的速度继续飞行，据测算到达目的地还需要15小时，问油箱中的油料是否够用？请说明理由．

正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上，分别连接BD、BF、FD，得到BFD.
（1）在图1、图2、图3中，若正方形CEFG的边长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：

图1                  图2                       图3

正方形CEFG的边长
1
3
4
BFD的面积
 
 
 
（2）若正方形CEFG的边长为，正方形ABCD的边长为，猜想的大小，并结合图3证明你的猜想.

《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来，就是类似地，图2所示的算筹图我们可以表述为（  ）

                         图1                    图2

    A．   B．     C．    D．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

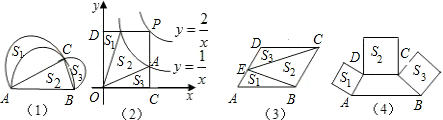
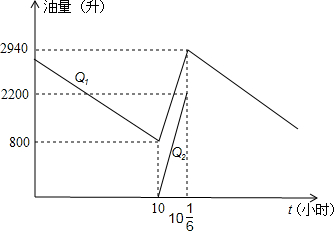精英家教网