Question

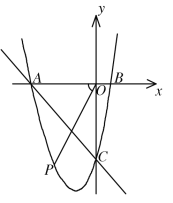
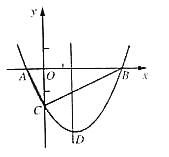
【题目】如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，且OC2=OA·OB.

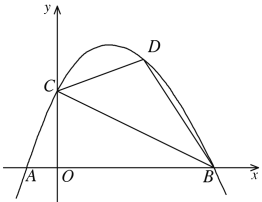
(1)证明：tan∠BAC· tan∠ABC=1;

(2)若点C的坐标为(0，2)，tan∠OCB=2，

①求该抛物线的表达式;

②若点D是该抛物线上的一点，且位于直线BC上方，当四边形ABDC的面积最大时，求点D的坐标.

Answer 1

【答案】（1）见解析；（2）①，②D.

【解析】

（1）由OC2=OA·OB和∠AOC=∠COB=90°，可判定△AOC∽△COB，可得∠BAC=∠OCB ，再根据正切的定义即可得证；

（2）①由C点坐标可得OC=2，然后由正切值求出OB，OA，即可得到A、B的坐标，然后采用待定系数法求函数表达式；

②连接AC，过D作DF⊥x轴，交直线BC于点E，设出D点坐标，先求出直线BC解析式，再根据D、E横坐标相同求出E点纵坐标，然后采用“铅锤法”可表示出△BCD的面积，因为△ABC固定，当△BCD面积最大时，则四边形ABDC面积最大.

解：（1）∵OC2=OA·OB

∴

∵∠AOC=∠COB=90°

∴△AOC∽△COB

∴∠BAC=∠OCB

∴tan∠BAC=tan∠OCB=

又∵tan∠ABC=

∴tan∠BAC· tan∠ABC=1

（2）①∵点C的坐标为(0，2)，tan∠OCB=2

∴OC=2，tan∠OCB==2

∴OB=2OC=4，则B点坐标为（4,0）

又∵OC2=OA·OB

∴OA=，则A点坐标为（-1,0）

将A（-1,0），B（4,0），C (0，2)代入二次函数表达式得，

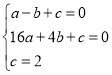，解得，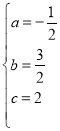

∴二次函数表达式为

②如图，连接AC，过D作DF⊥x轴，交直线BC于点E，

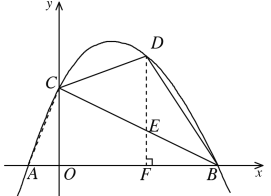
设BC直线解析式为，将B（4,0），C (0，2)代入得，

，解得，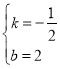

∴BC直线解析式为

设D点坐标为，

则E点横坐标为m，代入BC直线可得，

即E点坐标为

∴DE=

∴

∵S四边形ABDC=S△ABC+S△BCD，且S△ABC为定值，

∴当S△BCD取得最大值时，S四边形ABDC取得最大值.

∵

∴当m=2时，△BCD的面积最大值为4，此时S四边形ABDC取得最大值，

将x=2时，

∴当四边形ABDC的面积最大时，D的坐标为.