题目内容
已知方程x2+(m2-5)x+3=0的一个根是3,求m的值及方程的另一个根.
考点:一元二次方程的解,根与系数的关系
专题:
分析:将x=3代入原方程可求得m的值,将m的值代入原方程,解方程即可求得另一个根.
解答:解:∵方程x2+(m2-5)x+3=0的一个根是3,
∴方程9+3(m2-5)+3=0,
即m2-5=-4,
解得m=±1;
有方程x2-4x+3=0,
解得x1=3,x2=1.
所以另一根为1.
∴方程9+3(m2-5)+3=0,
即m2-5=-4,
解得m=±1;
有方程x2-4x+3=0,
解得x1=3,x2=1.
所以另一根为1.
点评:本题考查的是一元二次方程的解(根)的意义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.同时考查了一元二次方程的解法.

练习册系列答案
相关题目
-2,2,-4,-5,6这五个数中,任取两个数相乘,所得的积最大的是( )
| A、10 | B、20 | C、-30 | D、18 |
小华掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,则向上的一面的点数小于5的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
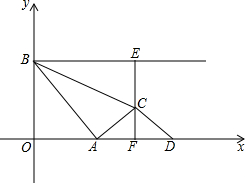 如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t.
如图,点A是x轴正半轴上的动点,点B的坐标为(0,4),将线段AB的中点绕点A按顺时针方向旋转90°得点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连接AC、BC、CD,设点A的横坐标为t. 已知,如图,在△ABC中,D是AB边上的一点,且BD=BC,BE⊥CD于点E,交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.
已知,如图,在△ABC中,D是AB边上的一点,且BD=BC,BE⊥CD于点E,交AC于点F,请再添加一个条件,使四边形DMCF是菱形,并加以证明.