题目内容
如图所示,数轴上有A、B、C三点,AC表示数轴A、C两点间的距离,且AB=3BC(即线段AB的长度为线段BC长度的3倍).

(1)若B为原点,A点表示数为6,求C点表示的数
(2)在(1)的条件下,若数轴上有一点P,且PC+PA=12,求P点表示的数.
若A、B、C三点代表的数为a、b、c,下列有两个结论:
①3c+a-4b的值不变
②3a+b-4c的值不变.
这两个结论中只有一个结论正确,请选择正确的结论加以说明,并求其不变值.
解:(1)∵AB=6,AB=2BC,
∴BC=2,
∴C表示的数是-2.
(2)设P表示的数是x,
分为两种情况:当P在C的左边时,
∵PA+PC=12,
∴6-x+(-2)-x=12,
x=-4,即此时P表示的数是-4;
当P在A的右边时,
∵PA+PC=12,
∴x-6+x-(-2)=12,
x=8,即P表示的数是8.
①3c+a-4b的值不变,
∵AB=3BC,A、B、C三点代表的数为a、b、c,
∴a=-3c,b=0,
∴3c+a-4b=3c+(-3c)+b=0,
即3c+a-4b的值不变,是0.
分析:(1)根据AB=6,AB=2BC求出BC=2,即可得出答案;
(2)设P表示的数是x,分为两种情况:当P在C的左边时,得出6-x+(-2)-x=12,当P在A的右边时得出x-6+x-(-2)=12,求出即可;
①值不变,是0.
点评:本题考查了数轴和有理数的计算的应用,主要考查学生的计算能力,用了转化思想.
∴BC=2,
∴C表示的数是-2.
(2)设P表示的数是x,
分为两种情况:当P在C的左边时,
∵PA+PC=12,
∴6-x+(-2)-x=12,
x=-4,即此时P表示的数是-4;
当P在A的右边时,
∵PA+PC=12,
∴x-6+x-(-2)=12,
x=8,即P表示的数是8.
①3c+a-4b的值不变,
∵AB=3BC,A、B、C三点代表的数为a、b、c,
∴a=-3c,b=0,
∴3c+a-4b=3c+(-3c)+b=0,
即3c+a-4b的值不变,是0.
分析:(1)根据AB=6,AB=2BC求出BC=2,即可得出答案;
(2)设P表示的数是x,分为两种情况:当P在C的左边时,得出6-x+(-2)-x=12,当P在A的右边时得出x-6+x-(-2)=12,求出即可;
①值不变,是0.
点评:本题考查了数轴和有理数的计算的应用,主要考查学生的计算能力,用了转化思想.

练习册系列答案
相关题目
 附加题:
附加题:
 如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.
如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.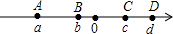 如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来.
如图所示,数轴上有四点A,B,C,D分别表示有理数a,b,c,d,用“<”把表示a,b,c,d,|a|,|b|,-|c|,-|d|的数连接起来. (1)已知|a-2|+|b+6|=0,则a+b=______.
(1)已知|a-2|+|b+6|=0,则a+b=______. ,
, ,
, ,将以上三个等式相加得:
,将以上三个等式相加得: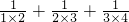 =1-
=1- +
+ +
+ =1-
=1- .
. =______.
=______. =______.
=______. -
- |+|
|+| -
-