题目内容
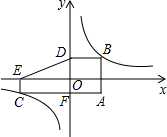 如图,过A(2,-1)分别作y轴、x轴的平行线交双曲线y=
如图,过A(2,-1)分别作y轴、x轴的平行线交双曲线y= 于点B、点C,交两坐标轴于点G、F,过点C作CE⊥x轴于点E,过点B作BD⊥y轴于点D,连接ED,若四边形AGOF的面积等于△EOD的面积,则实数k=________.
于点B、点C,交两坐标轴于点G、F,过点C作CE⊥x轴于点E,过点B作BD⊥y轴于点D,连接ED,若四边形AGOF的面积等于△EOD的面积,则实数k=________.
2
分析:先根据反比例函数y= 的图象判断出k的符号,再根据点A(2,-1)求出E、B两点的坐标,由S△ODE=S矩形AGOF=
的图象判断出k的符号,再根据点A(2,-1)求出E、B两点的坐标,由S△ODE=S矩形AGOF= ×
× ×k=2,即可得出结论.
×k=2,即可得出结论.
解答: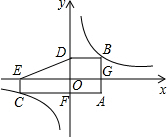 解:∵反比例函数y=
解:∵反比例函数y= 的图象在一、三象限,
的图象在一、三象限,
∴k>0,
∵点A(2,-1),CE⊥x轴于点E,BD⊥y轴于点D,
∴B(2, ),C(-k,-1),S矩形AGOF=2,
),C(-k,-1),S矩形AGOF=2,
∴CF=k,DO= ,
,
∴S△ODE=S矩形AGOF= ×
× ×k=2,
×k=2,
解得k=2 或k=-2
或k=-2 (舍去).
(舍去).
故答案为:2 .
.
点评:本题考查的是反比例函数系数k的几何意义,熟知在反比例函数y= 的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.
的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.

分析:先根据反比例函数y=
 的图象判断出k的符号,再根据点A(2,-1)求出E、B两点的坐标,由S△ODE=S矩形AGOF=
的图象判断出k的符号,再根据点A(2,-1)求出E、B两点的坐标,由S△ODE=S矩形AGOF= ×
× ×k=2,即可得出结论.
×k=2,即可得出结论.解答:
 解:∵反比例函数y=
解:∵反比例函数y= 的图象在一、三象限,
的图象在一、三象限,∴k>0,
∵点A(2,-1),CE⊥x轴于点E,BD⊥y轴于点D,
∴B(2,
 ),C(-k,-1),S矩形AGOF=2,
),C(-k,-1),S矩形AGOF=2,∴CF=k,DO=
 ,
,∴S△ODE=S矩形AGOF=
 ×
× ×k=2,
×k=2,解得k=2
 或k=-2
或k=-2 (舍去).
(舍去).故答案为:2
 .
.点评:本题考查的是反比例函数系数k的几何意义,熟知在反比例函数y=
 的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.
的图象上任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键. 
练习册系列答案
相关题目
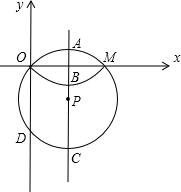 已知如图,过O且半径为5的⊙P交x的正半轴于点M(2m,0)、交y轴的负半轴于点D,弧OBM与弧OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点.
已知如图,过O且半径为5的⊙P交x的正半轴于点M(2m,0)、交y轴的负半轴于点D,弧OBM与弧OAM关于x轴对称,其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点.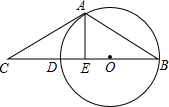 如图,过⊙O上一点A的切线AC与⊙O直径BD的延长线交于点C,过A作AE⊥BC于点E.
如图,过⊙O上一点A的切线AC与⊙O直径BD的延长线交于点C,过A作AE⊥BC于点E.
 点M,连接AM.已知PN=4.
点M,连接AM.已知PN=4. 如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )
如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )