题目内容
14.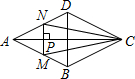 如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )
如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )| A. | 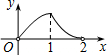 | B. | 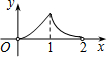 | C. | 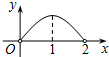 | D. |  |
分析 △CMN的面积=$\frac{1}{2}$CP×MN,通过题干已知条件,用x分别表示出CP、MN,根据所得的函数,利用其图象,可分两种情况解答:(1)0<x≤1;(2)1<x<2.
解答 解:(1)当0<x≤1时,如图1,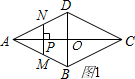
在菱形ABCD中,AC=2,BD=1,AO=1,且AC⊥BD;
∵MN⊥AC,∴MN∥BD;
∴△AMN∽△ABD,
∴$\frac{AP}{AO}=\frac{MN}{BD}$,
即$\frac{x}{1}=\frac{MN}{1}$,
∴MN=x,
∴y=$\frac{1}{2}$CP×MN=$\frac{1}{2}$$(2-x)x=-\frac{1}{2}{x}^{2}+x$(0<x≤1),
∵-$\frac{1}{2}$<0,∴函数图象开口向下;
(2)当1<x<2,如图2,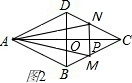
同理证得,△CDB∽△CNM,
$\frac{CP}{OC}=\frac{MN}{BD}$,
即$\frac{2-x}{1}=\frac{MN}{1}$,
∴MN=2-x,
∴y=$\frac{1}{2}$CP×MN=$\frac{1}{2}$(2-x)×(2-x)=$\frac{1}{2}(2-x)^{2}=\frac{1}{2}(x-2)^{2}$,
∵$\frac{1}{2}$>0,
∴函数图象开口向上;
综上,答案A的图象大致符合;
故选:A.
点评 本题考查了二次函数的图象,考查了学生从图象中读取信息的数形结合能力,体现了分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

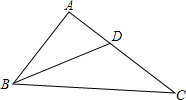 如图,在△ABC中,点D在AC上,且∠ABD=∠C.AB=6,AD=4.求线段CD的长.
如图,在△ABC中,点D在AC上,且∠ABD=∠C.AB=6,AD=4.求线段CD的长. 已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.
已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.