题目内容
16.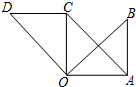 如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,把△OAB绕点O沿逆时针方向旋转90°,得到△OCD,连结AC.
如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,把△OAB绕点O沿逆时针方向旋转90°,得到△OCD,连结AC.(1)求证:四边形OACD是平行四边形;
(2)求四边形OACD的面积.
分析 (1)根据旋转的性质得AB=CD,∠AOC=90°,∠OCD=∠OAB=90°,则可判断OA∥CD,加上OA=AB,所以OA=CD,于是可判断四边形OACD是平行四边形;
(2)直接根据平行四边形的面积公式计算.
解答 (1)证明:∵△OAB绕点O沿逆时针方向旋转90°,得到△OCD,
∴AB=CD,∠AOC=90°,∠OCD=∠OAB=90°,
∴∠AOC=∠OCD,
∴OA∥CD,
又∵OA=AB,
∴OA=CD,
∴四边形OACD是平行四边形;
(2)四边形OACD的面积=OA•OC=6×6=36.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定与性质.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
7.下面计算正确的是( )
| A. | -x2-x2=0 | B. | 3a2+2a3=5a5 | C. | 3+x=3x | D. | -ab+ba=0 |
4.若x>y,则下列不等式成立的是( )
| A. | x-3<y-3 | B. | x+5>y+5 | C. | $\frac{x}{3}$<$\frac{y}{3}$ | D. | -2x>-2y |
11. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
 如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )
如图,AB是⊙O的直径,BC是⊙O的弦,若∠AOC=80°,则∠B的度数为( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
1.已知x=-2是方程x2-4x+c=0的一个根,则c的值是( )
| A. | -12 | B. | -4 | C. | 4 | D. | 12 |
8.若(x-2)(x+3)=x2-ax+b,则a、b的值是( )
| A. | a=5,b=6 | B. | a=1,b=-6 | C. | a=-1,b=-6 | D. | a=5,b=-6 |
5.点M(2,1)关于x轴对称的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (2,-1) | D. | (-1,2) |
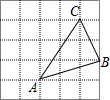 如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).
如图,每个小方格都是边长为1个单位的小正方形,A,B,C三点都是格点(每个小方格的顶点叫格点).