题目内容
 (1998•上海)已知△ABC中,AB=AC=6,cosB=
(1998•上海)已知△ABC中,AB=AC=6,cosB=| 1 | 3 |
(1)求证:直线EF是圆O的切线;
(2)求y关于x的函数解析式,并写出这个函数的定义域;
(3)当直线DF与圆O相切时,求OB的长.
分析:(1)首先连接OE,由AB=AC=6,易证得OE∥AC,又由EF⊥AC,即可证得直线EF是圆O的切线;
(2)求y关于x的函数关系式,可以证明△BOE∽△BAC,然后由相似三角形的对应边成比例,可用x表示出BE的长,又由三角函数的性质,即可求得y关于x的函数解析式,当圆与AC相切时可得OB的长,据此即可得到x的取值范围;
(3)首先连接OE,OF,DE,由EF、DF与⊙O相切,易证四边形OBCF是等腰梯形,得出OB=CF,得出方程,求出OB的长.
(2)求y关于x的函数关系式,可以证明△BOE∽△BAC,然后由相似三角形的对应边成比例,可用x表示出BE的长,又由三角函数的性质,即可求得y关于x的函数解析式,当圆与AC相切时可得OB的长,据此即可得到x的取值范围;
(3)首先连接OE,OF,DE,由EF、DF与⊙O相切,易证四边形OBCF是等腰梯形,得出OB=CF,得出方程,求出OB的长.
解答:(1)证明:如图1,连接OE,
∵OE=OB,
∴∠B=∠OEB.
∵AB=AC,
∴∠B=∠C.
∴∠OEB=∠C.
∴OE∥AC.
∵EF⊥AC,
∴EF⊥OE.
∵点E在⊙O上,
∴EF是⊙O的切线.
(2)解:如图2,作AH⊥BC,H为垂足,并连接OE,
∵AB=AC,
∴BH=
BC,
∵AB=6,cosB=
,
∴BH=2,
∴BC=4.
∵OE∥AC,
∴△BOE∽△BAC.
∴
=
.
即
=
.
∴BE=
x.
∴EC=4-
x.
在Rt△ECF中,cosC=cosB=
,
∴CF=EC•cosC=(4-
x)•
.
∴所求函数的关系式为y=
-
x.
 如图3,当⊙0与AC相切时,设切点为G,
如图3,当⊙0与AC相切时,设切点为G,
连接OE,OG,
∵EF是切线,
∴OE⊥EF,OG⊥AC,
∵EF⊥AC,
∴四边形OEFG是矩形,
∵OE=OG,
∴四边形OEFG是正方形,
即EF=OE=x,
∵cosC=
,
∴sinC=
,
∵在Rt△CEF中,sinC=
=
,
即
=
,
解得:x=
,
∴这个函数的定义域为:0<x<
;
(3)解:如图4,连接OE,DE,OF,
∵EF、DF与⊙O相切,
∴FD=FE,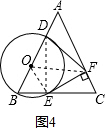 ∠DFO=∠EFO.
∠DFO=∠EFO.
∴OF垂直平分DE.
∵BD是直径,
∴∠DEB=90°,
∴BC⊥DE.
∴OF∥BC.
∴四边形OBCF是等腰梯形.
∴OB=CF,
得:
-
x=x,
解得:x=
.
即OB=
.
∵OE=OB,
∴∠B=∠OEB.
∵AB=AC,
∴∠B=∠C.
∴∠OEB=∠C.
∴OE∥AC.
∵EF⊥AC,
∴EF⊥OE.
∵点E在⊙O上,
∴EF是⊙O的切线.
(2)解:如图2,作AH⊥BC,H为垂足,并连接OE,
∵AB=AC,
∴BH=
| 1 |
| 2 |
∵AB=6,cosB=
| 1 |
| 3 |
∴BH=2,
∴BC=4.
∵OE∥AC,
∴△BOE∽△BAC.
∴
| BE |
| BC |
| OE |
| AC |
即
| BE |
| 4 |
| x |
| 6 |
∴BE=
| 2 |
| 3 |
∴EC=4-
| 2 |
| 3 |
在Rt△ECF中,cosC=cosB=
| 1 |
| 3 |
∴CF=EC•cosC=(4-
| 2 |
| 3 |
| 1 |
| 3 |
∴所求函数的关系式为y=
| 4 |
| 3 |
| 2 |
| 9 |
 如图3,当⊙0与AC相切时,设切点为G,
如图3,当⊙0与AC相切时,设切点为G,连接OE,OG,
∵EF是切线,
∴OE⊥EF,OG⊥AC,
∵EF⊥AC,
∴四边形OEFG是矩形,
∵OE=OG,
∴四边形OEFG是正方形,
即EF=OE=x,
∵cosC=
| 1 |
| 3 |
∴sinC=
2
| ||
| 3 |
∵在Rt△CEF中,sinC=
| EF |
| EC |
2
| ||
| 3 |
即
| x | ||
4-
|
2
| ||
| 3 |
解得:x=
216
| ||
| 49 |
∴这个函数的定义域为:0<x<
216
| ||
| 49 |
(3)解:如图4,连接OE,DE,OF,
∵EF、DF与⊙O相切,
∴FD=FE,
 ∠DFO=∠EFO.
∠DFO=∠EFO.∴OF垂直平分DE.
∵BD是直径,
∴∠DEB=90°,
∴BC⊥DE.
∴OF∥BC.
∴四边形OBCF是等腰梯形.
∴OB=CF,
得:
| 4 |
| 3 |
| 2 |
| 9 |
解得:x=
| 12 |
| 11 |
即OB=
| 12 |
| 11 |
点评:本题考查的是切线的判定与性质、切线长定理、相似三角形的判定与性质、正方形的判定与性质、等腰三角形的性质以及三角函数等知识.此题综合性很强,难度较大,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目