题目内容
如图,抛物线 :
: 的图象与两坐标轴分别交于
的图象与两坐标轴分别交于 三点,经过点
三点,经过点 (0,
(0, )的直线
)的直线 :
: 与x轴、抛物线的对称轴
与x轴、抛物线的对称轴 交于点
交于点 .
.
(1)填空: ;
; ;
;
(2)连结 .若
.若 ∽
∽ ,请求出抛物线
,请求出抛物线 的解析式;
的解析式;
(3)在(2)的条件下,把抛物线 向右平移1个单位后,向下平移
向右平移1个单位后,向下平移 个单位得到新的抛物
个单位得到新的抛物
线 .再将直线
.再将直线 绕着点
绕着点 进行旋转,当直线
进行旋转,当直线 与抛物线
与抛物线 相交于不同的两个交点
相交于不同的两个交点 时,过点
时,过点 (0,
(0, )、点
)、点 与点
与点 分别作直线
分别作直线 .猜想:直线
.猜想:直线 、
、 之间的位置关系(除相交于点
之间的位置关系(除相交于点 外).并请说明理由.
外).并请说明理由.
 |  | ||
解:(1)4;1 (2)∵ (0,
(0, ),
), 与抛物线的对称轴
与抛物线的对称轴 交于点
交于点
∴OE=2,OF=1.
∵ ∽
∽
 ∴OA=4
∴OA=4
即A(-4,0),B(2,0)
代入 可解得
可解得 ∴
∴
(3)直线 关于直线
关于直线 成轴对称。
成轴对称。
或直线 与直线
与直线 、直线
、直线 与直线
与直线 的夹角相等(相类似的也行)
的夹角相等(相类似的也行)
过点N作NH⊥y轴于点H,过点M作MG⊥y轴于点G


∴抛物线 的解析式为
的解析式为
由点 在直线
在直线 和抛物线
和抛物线 的图象上得:
的图象上得:

解得 ,
,
当 时,
时,
当 时,
时,
∴ ,
,
∴

∴
即
∴直线 关于直线
关于直线 成轴对称
成轴对称

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
记者小张要了解市民对“雾霾天气产生的主要成因”的看法,随机调查了某区的部分市民,并绘制了如下不完整的统计图表.请根据提供的信息解答下列问题:
(1)填空: ,
,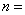 ;
;
(2)请求扇形统计图中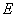 选项所占的百分比为 ;
选项所占的百分比为 ;
(3)若该区人口约有40万人,请估计其中持D选项“观点”的市民人数有多少人?
| 选项 | 观点 |
|
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 |
|
| C | 汽车尾气排放 |
|
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |

 cm B. 2
cm B. 2 cm C. 2
cm C. 2 cm D. 3cm
cm D. 3cm )cm.
)cm.

 频数(人数)
频数(人数)

 ),则点C的坐标为( )
),则点C的坐标为( )

 ,1) D. (﹣
,1) D. (﹣


 %,并写出该扇形所对圆心角的度数为 ,请补全条形图。
%,并写出该扇形所对圆心角的度数为 ,请补全条形图。