题目内容
如图,AB是⊙O的直径,点F,C是⊙O上两点,且 =
= =
= ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD=2 ,求⊙O的半径.
,求⊙O的半径.

(1)证明:连结OC,如图,
∵ =
= ,
,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
∴CD是⊙O的切线;
(2)解:连结BC,如图,
∵A B为直径,
B为直径,
∴∠ACB=90°,
∵ =
= =
= ,
,
∴∠BOC= ×180°=60°,
×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD=2 ,
,
∴AC=2CD=4 ,
,
在Rt△ACB中,BC= AC=
AC= ×4
×4 =4,
=4,
∴AB=2BC=4,
∴⊙O的半径为4.


练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处.若AD=3,BC=5,则EF的值是( )

|
| A. |
| B. | 2 | C. |
| D. | 2 |
2013年我国GDP总值为56.9万亿元,增速达7.7%,将56.9万亿元用科学记数法表示为( )
|
| A. | 56.9×1012元 | B. | 5.69×1013元 | C. | 5.69×1012元 | D. | 0.569×1013元 |
 =( )
=( ) D. ﹣
D. ﹣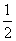 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.


 +(
+( ﹣1)0﹣
﹣1)0﹣ 的值为( )
的值为( )




 D.
D. 