题目内容
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②a+b+c>0;③c=﹣3a;④只有当a=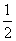 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
其中正确的结论是 .(只填序号)

③④.
【解析】

故①错误;
②根据图示知,当x=1时,y<0,即a+b+c<0.
故②错误;

∴△ADB为等腰直角三角形.
故④正确;
⑤要 使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,

∵由抛物线与y轴的交点在y轴的负半轴上 ,
,
∴c=﹣
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a= ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可 知只有两个a值满足条件.
知只有两个a值满足条件.
故⑤错误.
综上所述,正确的结论是③④.


练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
四边形ABCD中,对角线AC与BD交于点O,下列条件不能判定这个四边形是平行四边形的是( )
|
| A. | OA=OC,OB=OD | B. | AD∥BC,AB∥DC | C. | AB=DC,AD=BC | D. | AB∥DC,AD=BC |

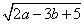 +(2a+3b﹣13)2=0,则此等腰三角形的周长为( )
+(2a+3b﹣13)2=0,则此等腰三角形的周长为( ) D⊥BC,垂足为点D,AN是△ABC外角
D⊥BC,垂足为点D,AN是△ABC外角 ∠CAM的平分线,CE⊥A
∠CAM的平分线,CE⊥A
 =
= =
= ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. ,求⊙O的半径.
,求⊙O的半径.