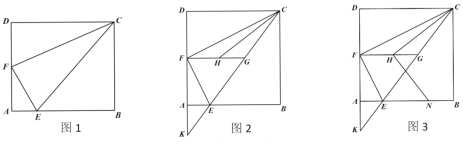
ЬтФПФкШн
ЁОЬтФПЁПдкМзЁЂввСНИіВЛЭИУїЕФПкДќжазАгажЪЕиЁЂДѓаЁЯрЭЌЕФаЁЧђЃЌМзДќжага2ИіАзЧђЃЌ1ИіЛЦЧђКЭ1ИіКьЧђЃКввДќжазАга1ИіАзЧђЃЌ1ИіЛЦЧђКЭШєИЩИіКьЧђЃЌДгввКажаЉвтУўШЁвЛЧђЮЊКьЧђЕФИХТЪЪЧДгМзКажаЉвтУўШЁвЛЧђЮЊКьЧђЕФИХТЪЕФ2БЖЃЎ
ЃЈ1ЃЉввДќжаКьЧђЕФИіЪ§ЮЊЁЁ ЃЎ
ЃЈ2ЃЉШєУўЕНАзЧђМЧ1ЗжЃЌУўЕНЛЦЧђМЧ2ЗжЃЌУўЕНКьЧђМЧ0ЗжЃЌаЁУїДгМзЁЂввСНДќжаЯШКѓЗжБ№ШЮвтУўШЁвЛЧђЃЌЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈЧѓаЁУїУўЕУСНИіЧђЕУ2ЗжЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉаЁУїУўЕУСНИіЧђЕУ2ЗжЕФИХТЪЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)ЪзЯШЩшввДќжаКьЧђЕФИіЪ§ЮЊxИіЃЌИљОнЬтвтПЩЕУЗНГЬЃК![]() ЃЌНтДЫЗНГЬМДПЩЧѓЕУД№АИЃЛ
ЃЌНтДЫЗНГЬМДПЩЧѓЕУД№АИЃЛ
(2)ЪзЯШИљОнЬтвтЛГіЪїзДЭМЃЌШЛКѓгЩЪїзДЭМЧѓЕУЫљгаЕШПЩФмЕФНсЙћгыаЁУїУўЕУСНИіЧђЕУ2ЗжЕФЧщПіЃЌдйРћгУИХТЪЙЋЪНЧѓНтМДПЩЧѓЕУД№АИЃЎ
(1)МзДќжаУўГіКьЧђЕФИХТЪЮЊ![]() ЃЌдђввДќжаУўГіКьЧђЕФИХТЪЮЊ
ЃЌдђввДќжаУўГіКьЧђЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
ЩшввДќжаКьЧђЕФИіЪ§ЮЊxИіЃЌ
ИљОнЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКxЃН2ЃЌ
ОМьбщЃЌxЃН2ЪЧдЗжЪНЗНГЬЕФНтЃЌ
ЁрввДќжаКьЧђЕФИіЪ§ЪЧ2ИіЃЌ
ЙЪД№АИЮЊЃК2ЃЛ
(2)ЛЪїзДЭМЕУЃК

ЁпЙВга16жжЕШПЩФмЕФНсЙћЃЌ
гжЁпУўЕНАзЧђМЧ1ЗжЃЌУўЕНЛЦЧђМЧ2ЗжЃЌУўЕНКьЧђМЧ0ЗжЃЌ
ЁраЁУїУўЕУСНИіЧђЕУ2ЗжЕФга5жжЧщПіЃЌ
ЁраЁУїУўЕУСНИіЧђЕУ2ЗжЕФИХТЪЮЊЃК![]() ЃЎ
ЃЎ

ЁОЬтФПЁПбЇаЃЮЊСЫЬсИпбЇЩњЬјдЖПЦФПЕФГЩМЈЃЌЖдШЋаЃ500УћОХФъМЖбЇЩњПЊеЙСЫЮЊЦквЛИідТЕФЬјдЖПЦФПЧПЛЏбЕСЗЃЎЭѕРЯЪІЮЊСЫСЫНтбЇЩњЕФбЕСЗЧщПіЃЌЧПЛЏбЕСЗЧАЃЌЫцЛњГщШЁСЫИУФъМЖВПЗжбЇЩњНјааЬјдЖВтЪдЃЌОЙ§вЛИідТЕФЧПЛЏбЕСЗКѓЃЌдйДЮВтЕУетВПЗжбЇЩњЕФГЩМЈЃЌНЋСНДЮВтЕУЕФГЩМЈжЦзїГЩШчЭМЫљЪОЕФЭГМЦЭМКЭВЛЭъећЕФЭГМЦБэ
бЕСЗКѓбЇЩњГЩМЈЭГМЦБэ
ГЩМЈ/ЗжЪ§ | 6Зж | 7Зж | 8Зж | 9Зж | 10Зж |
ШЫЪ§/ШЫ | 1 | 3 | 8 | 5 | n |
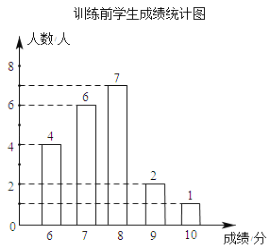
ИљОнвдЩЯаХЯЂЛиД№ЯТСаЮЪЬт
ЃЈ1ЃЉбЕСЗКѓбЇЩњГЩМЈЭГМЦБэжаn= ЃЌВЂВЙГфЭъГЩЯТБэЃК
ЦНОљЗж | жаЮЛЪ§ | жкЪ§ | |
бЕСЗЧА | 7.5 | 8 | |
бЕСЗКѓ | 8 |
ЃЈ2ЃЉШєЬјдЖГЩМЈ9ЗжМАвдЩЯЮЊгХауЃЌЙРМЦИУаЃОХФъМЖбЇЩњбЕСЗКѓБШбЕСЗЧАДяЕНгХауЕФШЫЪ§діМгСЫЖрЩйЃП