题目内容
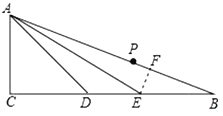
【题目】如图,![]() 中
中![]() 且
且![]() ,又
,又![]() 、
、![]() 为
为![]() 的三等分点.
的三等分点.

(1)求证![]() ;
;
(2)证明:![]() ;
;
(3)若点![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() 则使线段
则使线段![]() 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由)
【答案】(1)见解析;(2)见解析;(3)4.
【解析】
(1)利用勾股定理求得AD、DE的长,再根据BD、AD的长,利用两边对应相等,且夹角相等的两个三角形相似,即可判断;
(2)利用相似三角形的对应角相等以及三角形的外角的性质即可判断;
(3)作EF⊥AB于点F,利用△ABC∽△EBF,求得EF的长,即可确定PE的长的范围,从而求解.
解:(1)证明:∵![]() ,
,
∴![]() ,
,
∴在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(2)证明:∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)作![]() 于点
于点![]() .
.
在直角![]() 中,
中,![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() .
.
又∵![]() ,
,![]()
![]() ,
,
则![]() ,
,![]() 的整数值是1或2或3.
的整数值是1或2或3.
则当![]() 时,
时,![]() 的位置有2个;
的位置有2个;
当![]() 时,
时,![]() 的位置有1个;
的位置有1个;
当![]() 时,
时,![]() 的位置有1个.
的位置有1个.
故![]() 的整数点有4个.
的整数点有4个.
故答案是:4.

练习册系列答案
相关题目
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?



