题目内容
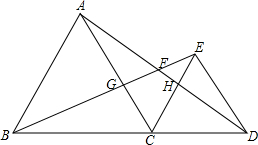 如图,C为线段BD上一点(不与点B,D重合),在BD同侧分别作正三角形ABC和正三角形CDE,AD与BE交于一点F,AD与CE交于点H,BE与AC交于点G.
如图,C为线段BD上一点(不与点B,D重合),在BD同侧分别作正三角形ABC和正三角形CDE,AD与BE交于一点F,AD与CE交于点H,BE与AC交于点G.(1)求证:BE=AD;
(2)求∠AFG的度数;
(3)求证:CG=CH.
分析:(1)根据等边三角形的性质得出AC=BC.CE=CD,∠ACB=∠ECD=60°,求出∠BCE=∠ACD,根据SAS证△BCE≌△ACD,推出AD=BE即可;
(2)利用(1)中的全等三角形的性质得到∠1=∠2.由三角形外角的定义得到:∠1+∠3=∠4=60°,则∠2+∠3=60°.根据三角形内角和定理可以求得∠AFG=60°;
(3)通过证明△ACH≌△BCG(ASA),来证得CG=CH(也可以通过证明△CGE≌△CHD).
(2)利用(1)中的全等三角形的性质得到∠1=∠2.由三角形外角的定义得到:∠1+∠3=∠4=60°,则∠2+∠3=60°.根据三角形内角和定理可以求得∠AFG=60°;
(3)通过证明△ACH≌△BCG(ASA),来证得CG=CH(也可以通过证明△CGE≌△CHD).
解答: (1)证明:∵△ABC和△DEC是等边三角形,
(1)证明:∵△ABC和△DEC是等边三角形,
∴AC=BC,CE=CD,∠4=∠5=60°,
∴∠4+∠6=∠5+∠6,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)解:∵由(1)知,△BCE≌△ACD,则∠1=∠2.
∵∠1+∠3=∠4=60°,
∴∠2+∠3=60°
∴∠AFG=60°;
(3)证明:∵∠4=∠5=60°
∴∠6=60°
∴∠6=∠4,
在△ACH与△BCG中,
,
∴△ACH≌△BCG(ASA),
∴CG=CH(也可以通过证明△CGE≌△CHD).
 (1)证明:∵△ABC和△DEC是等边三角形,
(1)证明:∵△ABC和△DEC是等边三角形,∴AC=BC,CE=CD,∠4=∠5=60°,
∴∠4+∠6=∠5+∠6,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)解:∵由(1)知,△BCE≌△ACD,则∠1=∠2.
∵∠1+∠3=∠4=60°,
∴∠2+∠3=60°
∴∠AFG=60°;
(3)证明:∵∠4=∠5=60°
∴∠6=60°
∴∠6=∠4,
在△ACH与△BCG中,
|
∴△ACH≌△BCG(ASA),
∴CG=CH(也可以通过证明△CGE≌△CHD).
点评:本题考查了全等三角形的判定与性质,等边三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
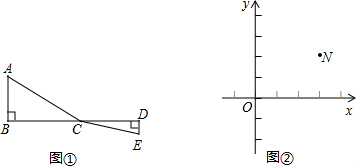
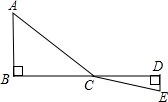 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,则AC+CE的最小值是
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,则AC+CE的最小值是 (2012•青田县模拟)为了探索代数式
(2012•青田县模拟)为了探索代数式 如图,C为线段BD上一点,BC=3,CD=2.△ABC、△ECD均为正三角形,AD交CE于F,则S△ACF:S△DEF的值为( )
如图,C为线段BD上一点,BC=3,CD=2.△ABC、△ECD均为正三角形,AD交CE于F,则S△ACF:S△DEF的值为( )