题目内容
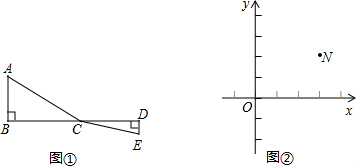
如图，C为线段BD上一点，BC=3，CD=2．△ABC、△ECD均为正三角形，AD交CE于F，则S△ACF：S△DEF的值为（ ）分析：由△ABC、△ECD均为正三角形，可证得AC∥DE，即可证得△ACF∽△DEF，然后由相似三角形面积比等于相似比的平方，求得S△ACF：S△DEF的值．
解答：解：∵△ABC、△ECD均为正三角形，BC=3，CD=2，
∴∠ACB=∠EDC=60°，AC=BC=3，DE=CD=2，
∴AC∥ED，
∴△ACF∽△DEF，
∴S△ACF：S△DEF=（
）2=（
）2=
．
故选C．
∴∠ACB=∠EDC=60°，AC=BC=3，DE=CD=2，
∴AC∥ED，
∴△ACF∽△DEF，
∴S△ACF：S△DEF=（
| AC |
| DE |
| 3 |
| 2 |
| 9 |
| 4 |
故选C．
点评：此题考查了相似三角形的判定与性质以及等边三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
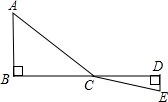如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=5，DE=1，BD=8，则AC+CE的最小值是
（2012•青田县模拟）为了探索代数式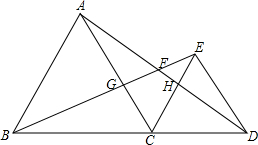
如图，C为线段BD上一点（不与点B，D重合），在BD同侧分别作正三角形ABC和正三角形CDE，AD与BE交于一点F，AD与CE交于点H，BE与AC交于点G．