Question

梯形ABCD中AB∥CD，∠ADC+∠BCD=90°，以AD、AB、BC为斜边向外作等腰直角三角形，其面积分别是S₁、S₂、S₃，且S₁+S₃=4S₂，则CD=（　　）

• A、2.5AB
• B、3AB
• C、3.5AB
• D、4AB

Answer 1

分析：过点B作BM∥AD，根据AB∥CD，求证四边形ADMB是平行四边形，再利用∠ADC+∠BCD=90°，求证△MBC为Rt△，再利用勾股定理得出MC²=MB²+BC²，在利用相似三角形面积的比等于相似比的平方求出MC即可．

解答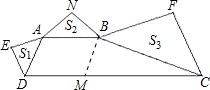：解：过点B作BM∥AD，
∵AB∥CD，∴四边形ADMB是平行四边形，
∴AB=DM，AD=BM，
又∵∠ADC+∠BCD=90°，
∴∠BMC+∠BCM=90°，即△MBC为Rt△，
∴MC²=MB²+BC²，
∵以AD、AB、BC为斜边向外作等腰直角三角形，
∴△AED∽△ANB，△ANB∽△BFC，

S1

S2

=

AD2

AB2

，

S2

S3

=

AB2

BC2

，
即AD²=

S1AB2

S2

，BC²=

S3AB2

S2

，
∴MC²=MB²+BC²=AD²+BC²=

S1AB2

S2

+=

S3AB2

S2

=

AB2(S1+S3)

S2

，
∵S₁+S₃=4S₂，
∴MC²=4AB²，MC=2AB，
CD=DM+MC=AB+2AB=3AB．
故选B．

点评：此题涉及到相似三角形的判定与性质，勾股定理，等腰直角三角形等知识点，解答此题的关键是过点B作BM∥AD，此题的突破点是利用相似三角形的性质求得MC=2AB，此题有一定的拔高难度，属于难题．