Question

（本题满分12分）（1）阅读合作学习内容，解答其中的问题；

合作学习 如图，矩形ABOD的两边OB，OD都在坐标轴的正半轴上，OD=3，另两边与反比例函数的图象分别相交于点E，F，且DE=2，过点E作EH⊥轴于点H，过点F作FG⊥EH于点G。回答下列问题： ①该反比例函数的解析式是什么？ ②当四边形AEGF为正方形时，点F的坐标是多少？

（2）小亮进一步研究四边形AEGF的特征后提出问题：“当AE>EG时，矩形AEGF与矩形DOHE能否全等？能否相似？”针对小亮提出的问题，请你判断这两个矩形能否全等？直接写出结论即可；这两个矩形能否相似？若能相似，求出相似比；若不能相似，试说明理由。

 

Answer 1

（1） ①y=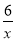 ②F（3,2）（2）不能全等 能相似 相似比为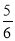

【解析】

试题分析：（1）根据矩形的性质和反比例函数的特点可以求出函数的解析式；再根据正方形的性质和反比例函数的特点求出F点的坐标；

（2）先假设全等，然后判断出F点不在反比例函数的图像上，判断出不全等；假设相似，得到相似的成比例线段，结合矩形的特点设出F点的坐标，根据反比例函数求出点F，从而求出相似比.

试题解析：（1）①∵四边形ABOD为矩形，EH⊥x，而OD=3，DE=2

∴E点的坐标为（2,3）

∴k=2×3=6

∴反比例函数的解析式为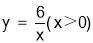

②设正方形AEGF的边长为a，则AE=AF=a

∴B点的坐标为（2+a，0），A点的坐标为（2+a，3）

∴F点的坐标为（2+a，3-a）

把F点代入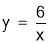，可得（2+a）（3-a）=6，

解得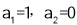（舍去）

∴F点的坐标为（3，2）

（2）①当AE＞EG时，矩形AECF与矩形DOHE不能全等.

理由：假设两矩形全等，则AE=OD=3，AF=DE=2，

∴A点的坐标为（5,3）

∴F点的坐标为（3,3）

而3×3=9≠6，F点不在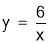上

故矩形AECF与矩形DOHE不能全等

②当AE＞EG时，若矩形AECF与矩形DOHE相似，根据相似的性质可得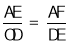

∴,

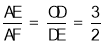设AE=3t，则AF=2t，得F点的坐标为（2+3t，3-2t），

所以由反比例函数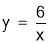可得（2+3t）（3-2t）=6，

解得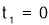（舍去），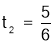

∴AE=3t=，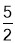

∴相似比为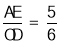

考点：反比例函数，矩形的性质，坐标与图形，矩形的相似