题目内容
如果设f(x)=| x2 |
| x2+1 |
| x2 |
| x2+1 |
| a2 |
| a2+1 |
| 12 |
| 12+1 |
| 1 |
| 2 |
(1)求f(2)+f(
| 1 |
| 2 |
(2)求f(x)+f(
| 1 |
| x |
(3)计算:f(1)+f(2)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
(结果用含有n的代数式表示,n为正整数)
分析:(1)把x=2和x=
代入所给解析式中,把得到的结果相加即可;
(2)把x和
代入解析式中的自变量,求得相应值,相加即可;
(3)把范例的结果和(2)中的结果应用到(3)中,相加即可.
| 1 |
| 2 |
(2)把x和
| 1 |
| x |
(3)把范例的结果和(2)中的结果应用到(3)中,相加即可.
解答:解:(1)当x=2时,f(2)=
,当x=
时,f(
)=
,
∴f(2)+f(
)=
+
=1;
(2)f(x)+f(
)=
+
=1;
(3)f(1)+f(2)+f(
)+f(3)+f(
)+…+f(n)+f(
)
=
+1×(n-1)=n-
.
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 5 |
∴f(2)+f(
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 5 |
(2)f(x)+f(
| 1 |
| x |
| x2 |
| x2+1 |
| 1 |
| x2+1 |
(3)f(1)+f(2)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
=
| 1 |
| 2 |
| 1 |
| 2 |
点评:解决本题的关键是找到相应的自变量以得到准确的函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
解方程x2-x+2=
时,如果设y=x2-x,那么原方程可变形为关于y的整式方程是( )
| 1 |
| x2-x |
| A、y2-2y-1=0 |
| B、y2-2y+1=0 |
| C、y2+2y+1=0 |
| D、y2+2y-1=0 |
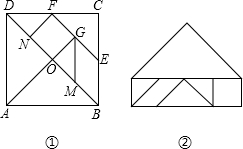 对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.
对正方形ABCD分划如图①,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.