Question

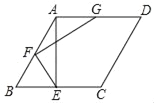
【题目】当题目条件出现角平分线时，我们往往可以构造等腰三角形解决问题．如图1，在△ABC中，∠A＝2∠B，CD 平分∠ACB，AD＝2，AC＝3，求 BC 的长．解决方法：如图 2，在BC 边上取点 E，使 EC＝AC，连接 DE．可得△DEC≌△DAC 且△BDE 是等腰三角形，所以 BC 的长为 5．试通过构造等腰三角形解决问题：如图 3，△ABC 中，AB＝AC，∠A＝20°，BD 平分∠ABC，要想求 AD 的长，仅需知道下列哪些线段的长（BC＝a， BD＝b， DC＝c）

A.a 和 bB.a 和 cC.b 和 cD.a、b 和 c

Answer 1

【答案】A

【解析】

作DE平分∠ADB与AB交于点E，在AD边上取点F，使，连接EF，通过证明和、△AEF是等腰三角形，可得和，从而得出我们只需知道线段BC和BD的长即可求出AD的长．

作DE平分∠ADB与AB交于点E，在AD边上取点F，使，连接EF

∵AB＝AC，∠A＝20°

∴

∵BD 平分∠ABC

∴

∵DE平分∠ADB与AB交于点E

∴

在△BDE和△FDE中

∴

∴

∴

∴

∴

∴

∴

∴

在△BCD和△BED中

∴

∴

∴

∴

∴只需知道线段BC和BD的长即可求出AD的长

故答案为：A．