题目内容
 如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,求∠BPC.
如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,求∠BPC.分析:根据三角形内角和定理以及角平分线的性质可求∠PBC+∠PCB的度数,从而求解.
解答:解:∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°.
又∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=
(∠ABC+∠ACB)=70°,
根据三角形内角和定理可知∠BPC=180°-(∠PBC+∠PCB)=110°.
∴∠BPC=110°.
∴∠ABC+∠ACB=180°-40°=140°.
又∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB=
| 1 |
| 2 |
根据三角形内角和定理可知∠BPC=180°-(∠PBC+∠PCB)=110°.
∴∠BPC=110°.
点评:本题考查的是三角形内角和定理以及角平分线的性质,此类题解题的关键是找出角平分线平分的两个角的和的度数,从而利用三角形内角和定理求解.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
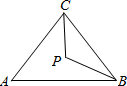 如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,∠BPC=
如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,∠BPC=
 如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,求∠BPC.
如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,求∠BPC. 如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,∠BPC=________.
如图:PC、PB是∠ACB、∠ABC的平分线,∠A=40°,∠BPC=________.