题目内容
如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍。
(1)问:这种设想能否实现?若能实现,请你设计一下;若不能,请说明理由;
(2)你设计的方案是什么图形,请说明理由。
(1)问:这种设想能否实现?若能实现,请你设计一下;若不能,请说明理由;
(2)你设计的方案是什么图形,请说明理由。
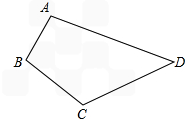
| 解:(1)能实现, ①连接AC、BD相交于O, ②分别过点A、C作BD的平行线; 分别过点B、D作AC的平行线.四条平行线组成一个四边形EFGH即为新的池塘(如图). (2)平行四边形 ∵EH∥BD,FG∥BD, ∴EH∥BD∥FG, 同理可得:EF∥AC∥HG, ∴四边形EFGH是平行四边形, 由上知四边形EBOA、OAHD、ODGC、0CFB都是平行四边形, 则S△ABO=S△EAB,S△BOC=S△BFC,S△OCD=S△GCD,S△AOD=S△AHD, 所以四边形EFGH的面积是四边形ABCD面积的2倍。 |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
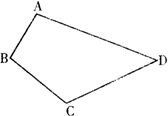 32、如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍
32、如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍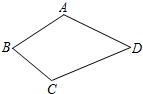 18、如图,某村有一个四边形的池塘,在它的四个顶点A、B、C、D处均有一棵树,该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持树不动,并要求扩建后的池塘成平行四边形形状,请问该村能否实现这一设想?
18、如图,某村有一个四边形的池塘,在它的四个顶点A、B、C、D处均有一棵树,该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持树不动,并要求扩建后的池塘成平行四边形形状,请问该村能否实现这一设想? 在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍
在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍