题目内容
3.化简和计算(1)$\frac{x^2}{x-2}-\frac{4x}{x-2}+\frac{4}{x-2}$
(2)(1-$\frac{2}{a-1}$)÷$\frac{{a}^{2}-6a+9}{{a}^{2}-a}$.
分析 (1)原式利用同分母分式的加减法则计算,约分即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=$\frac{{x}^{2}-4x+4}{x-2}$=$\frac{(x-2)^{2}}{x-2}$=x-2;
(2)原式=$\frac{a-3}{a-1}$•$\frac{a(a-1)}{(a-3)^{2}}$=$\frac{a}{a-3}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若y=(m-1)x|m|-2是反比例函数,则m的值为( )
| A. | m=2 | B. | m=-1 | C. | m=1 | D. | m=0 |
11.若a>b,则下列各式正确的是( )
| A. | ac>bc | B. | a2>b2 | C. | -2a<-2b | D. | a-2<b-2 |
13.若关于x的一元二次方程ax2+x+1=0有实数根,则a的取值范围是( )
| A. | a<$\frac{1}{4}$ | B. | a≤$\frac{1}{4}$且a≠0 | C. | a≥-$\frac{1}{4}$且a≠0 | D. | a≥-$\frac{1}{4}$ |
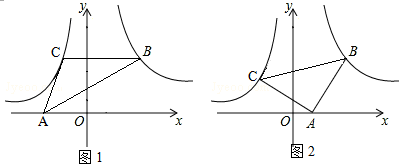
 点A(-1,2)和点B关于y轴对称,点C(2,1),
点A(-1,2)和点B关于y轴对称,点C(2,1),