Question

15．用棋子按下列方式摆图形，第一个图形有1枚棋子，第二个图形有5枚棋子，第三图形有11枚棋子，…依此规律，第7个图形棋子的个数为（　　）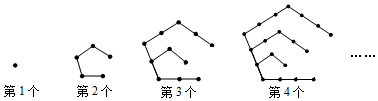

• A． 55
• B． 57
• C． 69
• D． 71

Answer 1

分析 根据图形可知：第一个图形有1枚棋子，第二个图形有1+4=5枚棋子，第三个图形有1+4+6=11枚棋子，第四个图形有1+4+6+8=19枚棋子，…，根据数的变化可找出变化规律“第n个图形有n²+n-1枚棋子”，依此规律即可得出结论．

解答 解：∵第一个图形有1枚棋子，第二个图形有1+4=5枚棋子，第三个图形有1+4+6=11枚棋子，第四个图形有1+4+6+8=19枚棋子，…，
∴第n个图形有1+4+6+…+2n=（2+n）（n-1）+1=n²+n-1枚棋子．
当n=7时，n²+n-1=7²+7-1=55．
故选A．

点评 本题考查了规律型中图形的变化类，根据图形中棋子数目的变化找出变化规律“第n个图形有n²+n-1枚棋子”是解题的关键．