题目内容
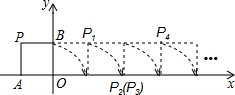 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3,…,P2013的位置,记Pi(xi,yi),i=1,2,3,…,2013,则P2013的横坐标x2013=
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2013次,点P依次落在点P1,P2,P3,…,P2013的位置,记Pi(xi,yi),i=1,2,3,…,2013,则P2013的横坐标x2013=考点:规律型:点的坐标
专题:
分析:观察规律可知纵坐标每4个一循环,可以判断P2013在503次循环后与P1纵坐标一致,以此可以求出P2013的横坐标,利用xn=xn+1时,则下一个点横坐标减1进而得出答案.
解答:解:根据规律:
P1(1,1),P2(2,0)=P3 ,P4(3,1)
P5(5,1),P6(6,0)=P7 ,P8(7,1)…
每4个一循环,可以判断P2013在503次循环后与P1纵坐标一致,坐标应该是(2013,1),
P2013的横坐标x2013=2013;如果xn=xn+1,则xn+2=n+1(请用含有n式子表示).
故答案为:2013; n+1.
P1(1,1),P2(2,0)=P3 ,P4(3,1)
P5(5,1),P6(6,0)=P7 ,P8(7,1)…
每4个一循环,可以判断P2013在503次循环后与P1纵坐标一致,坐标应该是(2013,1),
P2013的横坐标x2013=2013;如果xn=xn+1,则xn+2=n+1(请用含有n式子表示).
故答案为:2013; n+1.
点评:本题考查了点的坐标的规律变化,根据正方形的性质,判断出每翻转4次为一个循环组是解题的关键,要注意翻转一个循环组点P向右前行4个单位.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
下列语句中,不是命题的是( )
| A、对顶角相等 |
| B、直角的补角是直角 |
| C、过直线l外一点A作直线AB⊥l于点B |
| D、两个锐角的和是钝角 |
关于x,y的二元一次方程2x+3y=18的正整数解的个数为( )
| A、1 | B、2 | C、3 | D、4 |
下列运算正确的是( )
| A、a•a3=2a3 |
| B、(a2)3=a5 |
| C、a3÷a=a2 |
| D、a3 +a3=2a6 |
 如图,直线y=2x和y=ax+4交于点A,则不等式2x<ax+4的解集为( )
如图,直线y=2x和y=ax+4交于点A,则不等式2x<ax+4的解集为( )A、x<
| ||
| B、x<3 | ||
C、x>
| ||
| D、x>3 |