Question

如图(a)所示，有一块铁皮，拱形边缘呈抛物线状，MN＝4分米，抛物线顶点处到边MN的距离是4分米．要在铁皮下截下一矩形ABCD，使矩形顶点B，C落在边MN上，A，D落在抛物线上，问这样截下的矩形铁皮的周长能否等于8分米？(提示：以MN所在的直线为x轴建立适当的直角坐标系)

Answer 1

答案：
解析：

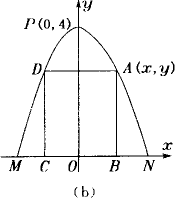
　　解：如图(b)所示，以边MN所在的直线为x轴，MN的中垂线为y轴建立直角坐标系．设抛物线的顶点为P，则点M，N，P的坐标依次为M(－2，0)，N(2，0)，P(0，4)．

　　由M，N，P三点坐标可得抛物线的解析式为y＝－x²＋4．

　　设A点坐标为(x，y)，

　　由AD＝BC＝2|x|，AB＝CD＝y．

　　∴矩形ABCD的周长l关于x的解析式l＝－2x²＋4|x|＋8．

　　函数l的自变量的取值范围是－2＜x＜2，且x≠0．

　　若l＝8，即－2x²＋2|x|＋8＝8，∴x²－2|x|＝0．

　　当x＞0时，x²－2x＝0，则，x＝0或x＝2；

　　当x＜0时，x²＋2x＝0，则x＝0或x＝－2．

　　∵－2＜x＜2，且x≠0，∴l的值不可能取8．

　　故截下的矩形周长不可能等于8分米．

　　思路点拨：建立恰当平面直角坐标系，得到抛物线解析式．

　　设出矩形与抛物线一个公共点坐标，用一个变量表示出矩形的周长．由周长等于8，得方程并解之得结论．

　　评注：这是一道抛物线与矩形综合的综合题，抛物线与平面几何中的图形结合的综合题是中考中的常见题型．这种类型的综合题的一般解法是通过建立恰当的平面直角坐标系，将几何问题转化为代数问题，然后通过代数方法的求解，而得到几何问题的解．这是一种数形结合思想的体现．解决这类题的关键是建立恰当的平面直角坐标系．对于抛物线来说，一般以其对称轴为y轴，建立相应的坐标系，开口向上向下由具体问题来确定．本题转化为一元二次方程来求解．

　　本题也可以以边MN所在的直线为x轴，点M为原点建立直角坐标系．这样建的优点是图形绝大部分处第一象限内，变量是非负值，可以避免讨论．当然本题的解法，也可以不失一般性设点的坐标为(x，y)，x＞0，y＞0这样也可以避免讨论，但还是要注意0＜x＜2，否则也会得到错误的结论．