题目内容
如图所示为一个污水净化塔内部，污水从上方入口进入后流经形如等腰直角三角形的净化材枓表面，流向如图中箭头所示，每一次水流流经三角形两腰的机会相同，经过四层净化后流入底部的5个出口中的一个．下列判断：①5个出口的出水量相同；②2号出口的出水量与4号出口的出水量相同；③1，2，3号出水口的出水量之比约为1：4：6；④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．其中正确的判断有（ ）个．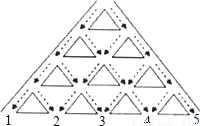
A．1个
B．2个
C．3个
D．4个
【答案】分析：根据出水量假设出第一次分流都为1，可以得出下一次分流的水量，依此类推得出最后得出每个出水管的出水量，进而得出答案．
解答：解：根据图示可以得出：
①根据图示出水口之间存在不同，故此选项错误；
②2号出口的出水量与4号出口的出水量相同；
根据第二个出水口的出水量为：[（
）÷2+
]÷2+
=
，
第4个出水口的出水量为：[（
）÷2+
]÷2+
=
，
故此选项正确；
③1，2，3号出水口的出水量之比约为1：4：6；
根据第一个出水口的出水量为：
，第二个出水口的出水量为：[（
）÷2+
]÷2+
=
，
第三个出水口的出水量为：
+
=
，
∴1，2，3号出水口的出水量之比约为1：4：6；故此选项正确；
④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．
∵1号与5号出水量为
，此处三角形材料损耗速度最慢，第一次分流后的水量为1（即净化塔最上面一个等腰直角三角形两直角边的水量为1），
∴净化塔最上面的三角形材料损耗最快，
故更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．
故此选项正确；
故正确的有3个．
故选：C．
点评：此题主要考查了可能性的大小问题，根据题意分别得出各出水口的出水量是解决问题的关键．
解答：解：根据图示可以得出：
①根据图示出水口之间存在不同，故此选项错误；
②2号出口的出水量与4号出口的出水量相同；
根据第二个出水口的出水量为：[（
）÷2+]÷2+=，第4个出水口的出水量为：[（
）÷2+]÷2+=，故此选项正确；
③1，2，3号出水口的出水量之比约为1：4：6；
根据第一个出水口的出水量为：
，第二个出水口的出水量为：[（）÷2+]÷2+=，第三个出水口的出水量为：
+=，∴1，2，3号出水口的出水量之比约为1：4：6；故此选项正确；
④若净化材枓损耗的速度与流经其表面水的数量成正比，则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．
∵1号与5号出水量为
，此处三角形材料损耗速度最慢，第一次分流后的水量为1（即净化塔最上面一个等腰直角三角形两直角边的水量为1），∴净化塔最上面的三角形材料损耗最快，
故更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．
故此选项正确；
故正确的有3个．
故选：C．
点评：此题主要考查了可能性的大小问题，根据题意分别得出各出水口的出水量是解决问题的关键．
练习册系列答案
相关题目
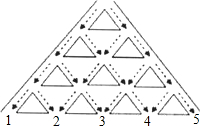角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍．其中正确的判断有（ ）个．