题目内容
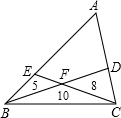
如图，在△ABC内的三个小三角形的面积分别为5，8，10，四边形AEFD的面积为x，则x=分析：连接AF，设S△AEF=a，S△ADF=b，根据三角形的面积与三角形底边成比例，进而求出四边形AEFD的面积．
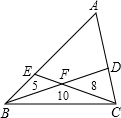
解答：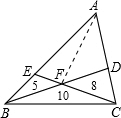
解：连接AF，设S△AEF=a，S△ADF=b，
∴
=
=
，
=
=
，
解得a=10，b=12，
∴四边形AEFD的面积x=a+b=22．
故答案为：22．
解：连接AF，设S△AEF=a，S△ADF=b，∴
| a |
| b+8 |
| EF |
| CF |
| 5 |
| 10 |
| b |
| a+5 |
| DF |
| BF |
| 8 |
| 10 |
解得a=10，b=12，
∴四边形AEFD的面积x=a+b=22．
故答案为：22．
点评：本题主要考查三角形的面积，根据等高的三角形的面积与底边成比例进行解答，需要同学们熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC内接于圆O，∠A=50°，∠ABC=60°，BD是圆O的直径，BD交AC于点E，连接DC，则∠AEB的度数等于
如图，在∠ABC内有一点P，问：能否在BA、BC边上各找一点M，N，使△PMN的周长最短？若能，请作图确定点M，N的位置（不需证明，不写作法，保留作图痕迹）；若不能，请说明理由．
如图，在△ABC内的三个小三角形的面积分别为5，8，10，四边形AEFD的面积为x，则x=________．