题目内容
3.为了预防控制登革热,某地计划租用甲、乙两辆汽车清理积水淤泥,从运输量估算,单独租用甲车比单独租用乙车清运少用5天完成任务,若租两车合运,则其完成时间是甲车单独完成时间的$\frac{3}{5}$.(1)甲、乙两车单独完成任务分别需要多少天?
(2)甲、乙两车合运3天后,因甲车故障须停运修理,余下任务由乙车完成,问乙车能否在5天内完成?若能,请说明理由;若不能,试求乙车至少须将其工作效率提高到原来的多少倍方可按时完成任务.
分析 (1)设甲车单独完成任务需要x天,乙单独完成需要x+5天,根据题意所述等量关系可得出方程组,解出即可;
(2)结合(1)的结论,求出剩余工作量,即可求出时间以及工作效率的倍数.
解答 解:(1)设甲车单独完成任务需要x天,乙单独完成需要(x+5)天,
根据题意得:$\frac{1}{x}+\frac{1}{x+5}=\frac{1}{\frac{3}{5}x}$,
解得:x=10,
经检验x=10是原方程的解,x+5=15,
答:甲、乙两车单独完成任务分别需要10天、15天;
(2)3($\frac{1}{10}$+$\frac{1}{15}$)=$\frac{1}{2}$,1-$\frac{1}{2}$=$\frac{1}{2}$,
$\frac{1}{2}$÷$\frac{1}{15}$=7.5(天)>5天,
即乙车不能在5天内完成;
$\frac{1}{2}$÷5=$\frac{1}{10}$,$\frac{1}{10}÷\frac{1}{15}$=1.5(倍),
即乙车至少须将其工作效率提高到原来的1.5倍方可按时完成任务.
点评 此题考查了分式方程的应用,及分式方程的解法;根据题意列出方程是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
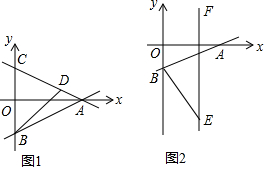 已知直线l1:y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点B,将直线沿x轴翻折,得到一个新函数的图象l2(图1),直线l2与y轴交于点C.
已知直线l1:y=$\frac{1}{2}$x-2与x轴交于点A,与y轴交于点B,将直线沿x轴翻折,得到一个新函数的图象l2(图1),直线l2与y轴交于点C.