Question

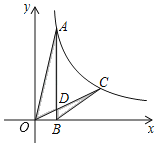
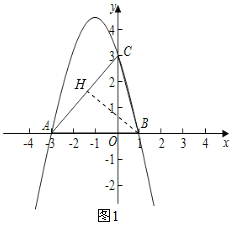
【题目】如图，抛物线与x轴相交于点A（﹣3，0）、点B（1，0），与y轴交于点C（0，3），点D是抛物线上一动点，联结OD交线段AC于点E．

（1）求这条抛物线的解析式，并写出顶点坐标；

（2）求∠ACB的正切值；

（3）当△AOE与△ABC相似时，求点D的坐标．

Answer 1

【答案】（1）y＝﹣x2﹣2x+3，所以该抛物线的顶点坐标是（﹣1，4）；（2）2；（3）点D的坐标是（，）或（﹣，2）

【解析】

（1）利用待定系数法确定函数解析式，根据函数解析式求得该抛物线的顶点坐标；

（2）过点B作BH⊥AC于点H，构造直角和直角，利用勾股定理及两点间的距离公式求得相关线段的长度，从而利用锐角三角函数的定义求解即可；

（3）过点D作DK⊥x轴于点K，构造直角，设，则并由题意可知点D位于第二象限，由于是公共角，所以当与相似时，有2种情况：①，即，由锐角三角函数的定义列出比例式，即可得到D点坐标，②，即，由锐角三角函数的定义列出比例式，即可得到D点坐标.

解：（1）设抛物线解析式为：，将点，，分别代入得：

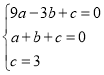，解得：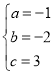

故抛物线解析式为：

由于

所以该抛物线的顶点坐标是；

（2）如图1，过点B作BH⊥AC于点H

∵，OA＝OC＝3

∴，

∵

∴

∴

∵在直角中，，AB＝4

∴

∴

∵

∴；

（3）如图2，过点D作DK⊥x轴于点K

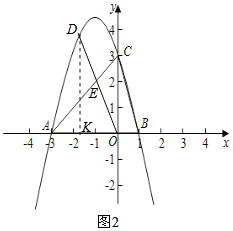
设，则．并由题意知点D位于第二象限

∴，

∵∠BAC是公共角

∴当与相似时，有2种情况：

①∠AOD＝∠ABC

∴

∴＝3，解得x1＝，x2＝，经检验当x1＝，x2＝时原分式方程有意义

∵点D位于第二象限

∴x2＝舍去

∴；

②∠AOD＝∠ACB

∴

∴＝2，解得，，经检验当，时原分式方程有意义

∵点D位于第二象限

∴舍去

∴

综上所述，当与相似时，求点D的坐标是或．