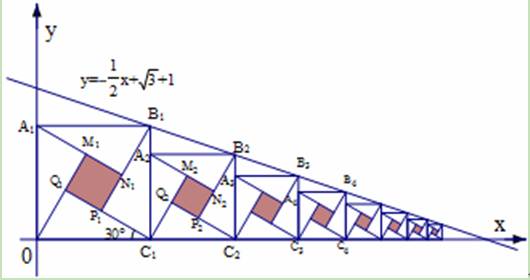
题目内容
2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线 和x轴上,则第n个阴影正方形的面积为 .
和x轴上,则第n个阴影正方形的面积为 .
【答案】分析:根据阴影正方形的边长与大正方形边长有个对应关系,分别表示出每个阴影部分的面积,得出规律,即可得出第n个阴影正方形的面积.
解答:解:∵B1点坐标设为(t,t),
∴t=- t+
t+ +1,
+1,
解得:t= (
( ),
),
∴B1N1= t=
t= (
( +1),那么大正方形边长为t,
+1),那么大正方形边长为t,
阴影正方形边长为 t-
t- t=
t= ×
× (
( )=
)= ,
,
∴第1个阴影正方形的面积是( )2,
)2,
∴每个相邻正方形中多边形,可以理解成是一系列的相似多边形,相似比为2:3,
∴第2个阴影正方形的面积为:( •
• )2=(
)2=( )4,
)4,
第3个阴影正方形的面积为:( •
• •
• )2=(
)2=( )6,
)6,
∴第n个阴影正方形的面积为:( )2n,
)2n,
故答案为:( )2n.
)2n.
点评:此题主要考查了勾股定理以及正方形的性质和一次函数的综合应用,得出相似多边形,相似比为2:3,进而得出正方形面积是解决问题的关键.
解答:解:∵B1点坐标设为(t,t),
∴t=-
 t+
t+ +1,
+1,解得:t=
 (
( ),
),∴B1N1=
 t=
t= (
( +1),那么大正方形边长为t,
+1),那么大正方形边长为t,阴影正方形边长为
 t-
t- t=
t= ×
× (
( )=
)= ,
,∴第1个阴影正方形的面积是(
 )2,
)2,∴每个相邻正方形中多边形,可以理解成是一系列的相似多边形,相似比为2:3,
∴第2个阴影正方形的面积为:(
 •
• )2=(
)2=( )4,
)4,第3个阴影正方形的面积为:(
 •
• •
• )2=(
)2=( )6,
)6,∴第n个阴影正方形的面积为:(
 )2n,
)2n,故答案为:(
 )2n.
)2n.点评:此题主要考查了勾股定理以及正方形的性质和一次函数的综合应用,得出相似多边形,相似比为2:3,进而得出正方形面积是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 14、如图是2002年在北京召开的世界数学家大会的会标,其中央图案正是经过艺术处理的“弦图”,它蕴含着一个著名的定理是
14、如图是2002年在北京召开的世界数学家大会的会标,其中央图案正是经过艺术处理的“弦图”,它蕴含着一个著名的定理是 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽弦图为基础设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cosθ的值等于
2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽弦图为基础设计的,弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cosθ的值等于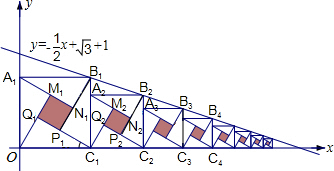 2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线
2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形,中间的阴影部分是一个小正方形的“赵爽弦图”.若这四个全等的直角三角形有一个角为30°,顶点B1、B2、B3、…、Bn和C1、C2、C3、…、Cn分别在直线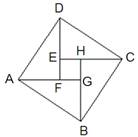
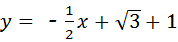 和x轴上,则第n个阴影正方形的面积为
和x轴上,则第n个阴影正方形的面积为