Question

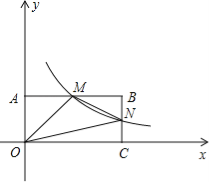
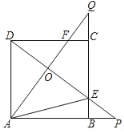
【题目】如图，正方形ABCD的边长是3，延长AB至点P、延长BC至点Q，使BP＝CQ，连接AQ，DP交于点O，相Q交CD于点F，DP交BC于点E，连接AE．

（1）求证：AQ⊥DP；

（2）求证：S△AOD＝S四边形OECF；

（3）当BP＝1时，请直接写出OE：OA的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

（1）由四边形ABCD是正方形，得到AD＝BC，∠DAB＝∠ABC＝90°，根据全等三角形的性质得到∠P＝∠Q，根据余角的性质得到AQ⊥DP；

（2）证明△CQF≌△BPE，根据全等三角形的性质得到CF＝BE，DF＝CE，于是得到S△ADF﹣S△DFO＝S△DCE﹣S△DOF，即S△AOD＝S四边形OECF；

（3）证明△PBE∽△PAD，根据相似三角形的性质得到BE＝，求出QE＝，OQ＝，OE＝，即可求出OE：OA的值．

（1）证明：∵四边形ABCD是正方形，

∴AD＝BC，∠DAB＝∠ABC＝90°，

∵BP＝CQ，

∴AP＝BQ，

在△DAP与△ABQ中，

，

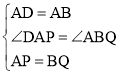∴△DAP≌△ABQ（SAS），

∴∠P＝∠Q，

∵∠Q+∠QAB＝90°，

∴∠P+∠QAB＝90°，

∴∠AOP＝90°，

∴AQ⊥DP；

（2）证明：在△CQF与△BPE中，

，

∴△CQF≌△BPE（ASA），

∴CF＝BE，

∴DF＝CE，

在△ADF与△DCE中，

，

∴△ADF≌△DCE（SAS），

∴S△ADF﹣S△DFO＝S△DCE﹣S△DOF，

∴S△AOD＝S四边形OECF；

（3）解：∵BP＝1，AB＝3，

∴PA＝4，

∵△PBE∽△PAD，

∴，

∴，

∴QE＝CQ+BC﹣CE＝1+3﹣，

∵AD∥QE，

∴△QOE∽△PAD，

∴，

∴OQ＝，OE＝，

∴，

∴．