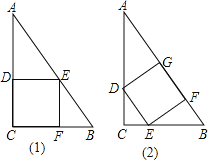
题目内容
【题目】如图,将边长为8的等边![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,过点
轴正半轴上,过点![]() 作
作![]() 于点
于点![]() ,将
,将![]() 绕着原点
绕着原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,这时,点
,这时,点![]() 恰好落在
恰好落在![]() 轴上.若动点
轴上.若动点![]() 从原点
从原点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为
运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为![]() 秒.
秒.
(1)请直接写出点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 的值;
的值;
(3)设![]() 与
与![]() 相交于点
相交于点![]() ,当
,当![]() 为何值时,
为何值时, ![]() 与
与![]() 相似?
相似?

【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 秒或
秒或![]() 秒时,
秒时, ![]() 与
与![]() 相似.
相似.
【解析】试题分析:(1)根据等边三角形的性质可直接得出A点坐标;再由OC⊥AB可得出OC的长,根据图形旋转不变性的性质可得出OD的长,进而得出D点坐标;
(2)过点E作EG⊥OD于点G,根据等边三角形的性质可知OC平分∠AOB,再根据锐角三角函数的定义求出EG的长,S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t即可得出t的值;
﹣t即可得出t的值;
(3)由于∠BOD=∠FOP,△OPF∽△ODB和△OPF∽△OBD两种情况进行讨论.
试题解析:解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,∴A(8,0),∵OC⊥AB,∴∠AOC=30°,∴OC=OAcos30°=8×![]() =
=![]() ,∵△OAC旋转后OC与OD重合,∴D(0,
,∵△OAC旋转后OC与OD重合,∴D(0, ![]() );
);
(2)过点E作EG⊥OD于点G,如图①所示:
∵△OAB为等边三角形,OC⊥AB,∴OC平分∠AOB,∴∠AOC=30°,∴∠EOG=90°﹣30°=60°,∴EG=OEsin∠EOG=![]() t,又∵S△OEF=
t,又∵S△OEF=![]() OFEG,OF=OD﹣DF=
OFEG,OF=OD﹣DF=![]() ﹣t,由题意可得:
﹣t,由题意可得: ![]() (
(![]() ﹣t)
﹣t)![]() t=
t=![]() ,解得t=
,解得t=![]() ±3;
±3;
(3)因为∠BOD=∠FOP,所以应分两种情况讨论:
①当∠FPO=∠BDO=90°时,如图②,∵△OPF∽△ODB,此时OE=OF,∴t=![]() ﹣t,解得:t=
﹣t,解得:t=![]() ;
;
②当∠OFP=∠ODB=90°时,如图③,∵△OPF∽△OBD,∴OF=![]() OE,即(
OE,即(![]() ﹣t)=
﹣t)=![]() t,解得:t=
t,解得:t=![]() .
.
综上所述,当t=![]() 秒或t=
秒或t=![]() 秒时,△OPF与△OBD相似.
秒时,△OPF与△OBD相似.


 通城学典默写能手系列答案
通城学典默写能手系列答案