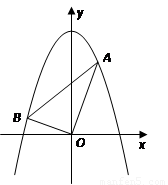题目内容
已知:直线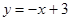 交
交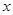 轴于点
轴于点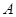 ,交
,交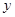 轴于点
轴于点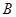 ,抛物线
,抛物线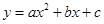 经过
经过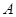 、
、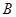 、
、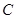 (1,0)三点.
(1,0)三点.
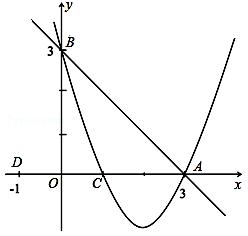
(1)求抛物线的解析式;
(2)若点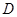 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线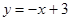 上有一点
上有一点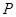 ,使
,使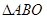 与
与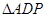 相似,求出点
相似,求出点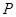 的坐标;
的坐标;
(3)在(2)的条件下,在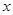 轴下方的抛物线上,是否存在点
轴下方的抛物线上,是否存在点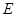 ,使
,使 的面积等于四边形
的面积等于四边形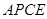 的面积?如果存在,请求出点
的面积?如果存在,请求出点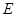 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(1) ;(2)
;(2)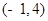 或(1,2);(3)不存在
或(1,2);(3)不存在
【解析】
试题分析:(1)先求得直线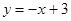 与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;
与坐标轴的交点A、B的坐标,再由抛物线经过A、B、C三点即可根据待定系数法求得结果;
(2)由题意可得:△ABO为等腰直角三角形,分△ABO∽△AP1D,△ABO∽△ADP2,根据等腰三角形的性质及相似三角形的性质求解即可;
(3)如图设点E 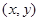 ,根据三角形的面积公式可得
,根据三角形的面积公式可得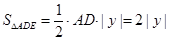 ①当P1(-1,4)时,
①当P1(-1,4)时,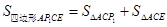
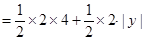 =
= 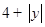 ,由点E在x轴下方可得
,由点E在x轴下方可得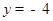 ,代入得
,代入得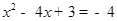 即
即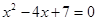 ,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,
,根据△=(-4)2-4×7=-12<0可得此方程无解;②当P2(1,2)时,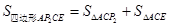 =
= 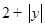 ,由点E在x轴下方可得
,由点E在x轴下方可得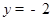 ,代入得:
,代入得: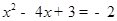 ,即
,即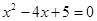 ,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.
,根据△=(-4)2-4×5=-4<0可得此方程无解,综上所述,在x轴下方的抛物线上不存在这样的点E.
(1)由题意得,A(3,0),B(0,3)
∵抛物线经过A、B、C三点,
∴把A(3,0),B(0,3),C(1,0)三点分别代入 得方程组
得方程组
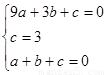 ,解得:
,解得: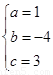
∴抛物线的解析式为 ;
;
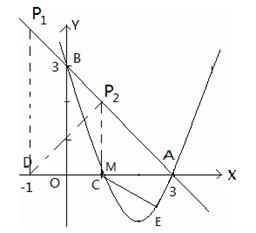
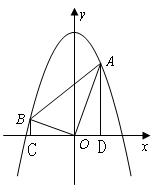
(2)由题意可得:△ABO为等腰直角三角形,如图所示
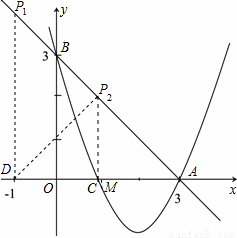
若△ABO∽△AP1D,则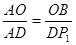
∴DP1=AD=4
∴P1
若△ABO∽△ADP2 ,过点P2作P2 M⊥x轴于M,AD=4
∵△ABO为等腰三角形
∴△ADP2是等腰三角形,由三线合一可得:DM="AM=2=" P2M,即点M与点C重合
∴P2(1,2);
(3)如图设点E  ,则
,则
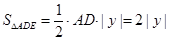
①当P1(-1,4)时,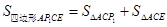
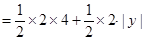 =
= 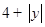
∴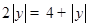 ,
,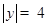
∵点E在x轴下方
∴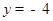 ,代入得
,代入得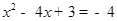 即
即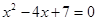
∵△=(-4)2-4×7=-12<0
∴此方程无解;
②当P2(1,2)时,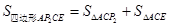 =
= 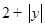
∴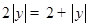 ,
,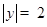
∵点E在x轴下方
∴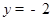 ,代入得:
,代入得: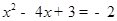 ,即
,即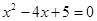 ,
,
∵△=(-4)2-4×5=-4<0
∴此方程无解
综上所述,在x轴下方的抛物线上不存在这样的点E.
考点:二次函数的综合题
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

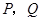 两点,问是否存在直线
两点,问是否存在直线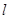 对应的函数关系式;若不存在,请说明理由.
对应的函数关系式;若不存在,请说明理由.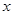 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点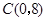 .
.
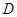 的坐标;
的坐标; 交
交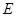 .在线段
.在线段 的垂直平分线上是否存在点
的垂直平分线上是否存在点 ,使得点
,使得点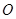 的距离?如果存在,求出点
的距离?如果存在,求出点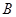 作
作 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?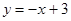 交
交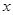 轴于点
轴于点 ,交
,交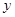 轴于点
轴于点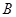 ,抛物线
,抛物线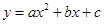 经过
经过 (1,0)三点.
(1,0)三点.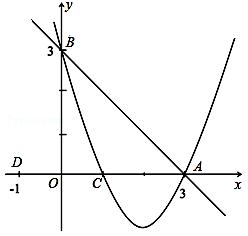
 的坐标为(-1,0),在直线
的坐标为(-1,0),在直线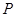 ,使
,使 与
与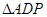 相似,求出点
相似,求出点 ,使
,使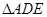 的面积等于四边形
的面积等于四边形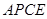 的面积?如果存在,请求出点
的面积?如果存在,请求出点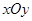 中,点
中,点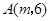 ,
,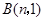 为两动点,其中
为两动点,其中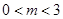 ,连结
,连结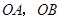 ,
,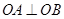 .
.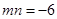 ;
;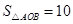 时,抛物线经过
时,抛物线经过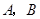 两点且以
两点且以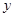 轴为对称轴,求抛物线对应的二次函数的关系式;
轴为对称轴,求抛物线对应的二次函数的关系式;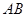 交
交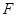 ,过点
,过点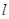 交抛物线于
交抛物线于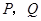 两点,问是否存在直线
两点,问是否存在直线 ?若存在,求出直线
?若存在,求出直线